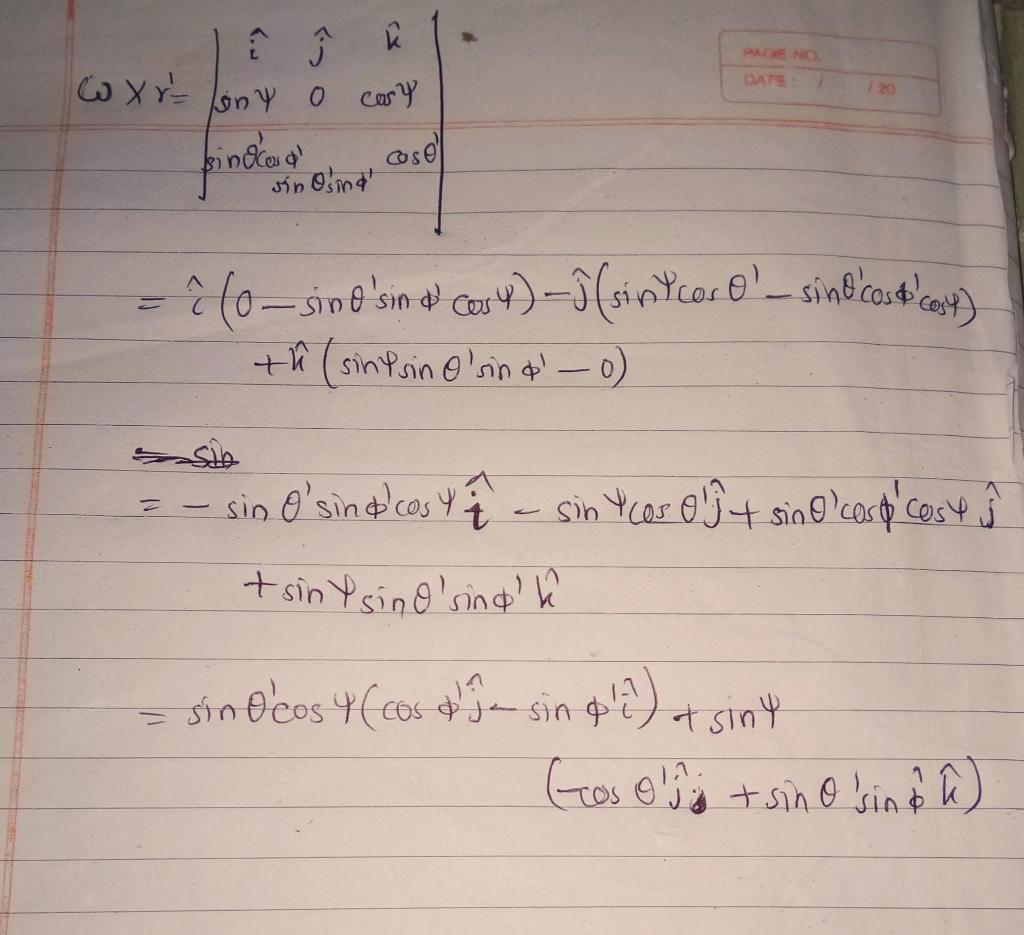
Solve the following problem with MATLAB. Plot whatever is necessary. Show the program you made to graph and solve the problem. Magnetic ball. A spherical shell of radius R, carries a surface uniform charge o and rotates with an angular velocity w. We wish to find the vector magnetic potential at an arbitrary point r in space. For this, we first rotate our reference system such that the position r is on the z axis and that the angular velocity w is in the xz plane as seen in the image. w Y ' Figure 1: Rotating spherical shell with surface charge density o. Using the integral form of the potential vector on a surface K(r') A(r) 47 -DA'. (1) rd where K(r') is the surface current density given by K(r') = ov', while ra= VR2 + p2 2Rr cos O' and dA' = R2 sin O'd0'do'. (a) To find v 'we must obtain w x r'. Calculate numerically the cross product of w = w (sin, 0, cosy)) with r = R (sin O'cosa', sin sind', cos'). PRENO W or any o DATE cary pindad in osell sin Osind - ? (osind sin & Cosy) f sint cor O'_ sind cost cosy) ti (sintsin O'rindo) - t - - sin o'sind cosy - sint cos o t sino caso cost 5 + sint sind sind - sino'cos 4 (costa sin pl) at siny Gosols + sino sin b