. Kindly solve the following attachment.

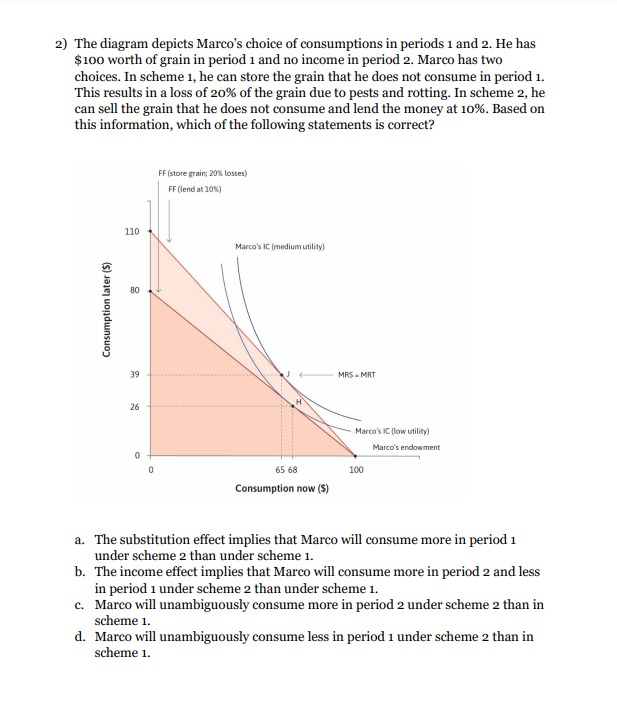
Q2. [14 points] Consider the same simple linear regression (SLR) model in Q1 which satises Gauss Markov assumptions: Y = ,80 + ,81 X + u, where the error term u has an unconditional variance of oz. Your friend highly recommends this specic linear estimator Z3: = 2:21 wil'i, where 1 W = _ 1 x2-x1 w _ 1 2 552351 w; = 0 for i = 3,4,5, ...., n, where n is the sample size. (a) (6 points) Is this estimator bias or unbiased? Please prove. (b) (8 points) Derive the conditional variance of this estimator B: Is it greater or less than the .._. 2 conditional variance of OLS estimator )31 derived in class, i.e. m1? i=1 I: Hint.' You willnd that your work in Q1 are usecl in this question. 1. (3 points) In Metropolis only taxicabs and privately owned automobiles are allowed to use the highway betwem the airport and downtown. The market for taxi cab service is competitive. There is a special lane for taxicabs, so taxis are always able to travel at 55 miles per hour. The demand for trips by taxi cabs depends on the taxi fare P, the average speed of a trip by private automobile on the highway E, and the price of gasoline G. The number of trips supplied by taxi cabs will depend on the taxi fare and the price of gasoline. Suppose the demand for trips by taxi is given by the equation 9* = 1000 + 50G - 4E - 4001\". The supply of trips by taxi is given by the equation 9' = 200 - 306 + 1001'. When G = 4 and E =30, nd equilibrium taxi fare. At equilibrium, what is the cross-price elasticity between gasoline and taxi cab service. 2. (2 points) Ray buys only hamburgers and bottles of root beer out of a weekly income of $100. He currently consumes 20 bottles of root beer per week, and his marginal utility ofroct bow is 6. The price ofroet beer is $2 per bottle. Currently, he also consumes 15 hamburgers per week, and his marginal utility of a hamburger is 8. Is Ray maximizing utility at his current consumption basket? If not, should he buy more hamburgers each week, or fewer? 3. (2 points) Helen's preferences over CDs {C} and sandwiches (.5) are given by DIS, C) = SC+10(S+ C), wiiMU6=S+ 10 andMUs= C+ 10.1fthe price ofaCD is $9 andthe price of a sandwich is $3, and Helen can spend a combined total of $30 each day on these goods, nd Helen's optimal consumption basket. 4. (8 points) Lou's preferences over pizza (x) and other goods (12) are given by U(x, y} = xy, with associated marginal utilities MU: = y and 1111)} = x. :1) Calculate his optimal basket as a function of Px, Py and income. {2 points) b) When P; = 1, his income is $120, calculate his income and substitution effects of a decrease in the price of food P; 'crn $4 to $3. (2 points) c) When P}! = 1, his income is $120, calculate the compensating variation of a decrease in the price of food P: from $4 to $3. (2 points} d) When P} = 1, his income is $120, calculate the equivalent variation of a decrease in the price of food Px from $4 to $3. (2 points} EXERCISES 1. Decide which of the following spaces are compact. If practicable, sketch a picture of the space. The set R of real numbers, the plane R?, or any sub- space of these spaces will be assumed to have the usual metric topology. Products will have the product topology. *) (0, 1) X [0, 1] bj C X R, where C - {(z, y) ( x' + y" = 1} cR () ((, vz) |itytz = l}CR d) ((, y) |x'ty4 0, J(z) = 0 if z = 0. Prove that f is not continuous. [Hint: Suppose f is a continuous function from a compact space X onto a compact space Y. Define Gy - {(z, y) | y = f(z)). Prove that if is continuous, then Gy is a closed subset of the product space X X Y. The proof through Proposition 10. Chap-2) The diagram depicts Marco's choice of consumptions in periods 1 and 2. He has $100 worth of grain in period i and no income in period 2. Marco has two choices. In scheme 1, he can store the grain that he does not consume in period 1. This results in a loss of 20% of the grain due to pests and rotting. In scheme 2, he can sell the grain that he does not consume and lend the money at 10%. Based on this information, which of the following statements is correct? FF (store grain; 20% losses) FF (lend at 10%) 110 Marco's IC (medium utility) Consumption later ($) 39 MRS - MRT 26 Marco's IC (low utility) Marco's endowment 65 68 100 Consumption now ($) a. The substitution effect implies that Marco will consume more in period 1 under scheme 2 than under scheme 1. b. The income effect implies that Marco will consume more in period 2 and less in period 1 under scheme 2 than under scheme 1. c. Marco will unambiguously consume more in period 2 under scheme 2 than in scheme 1. d. Marco will unambiguously consume less in period 1 under scheme 2 than in scheme 1