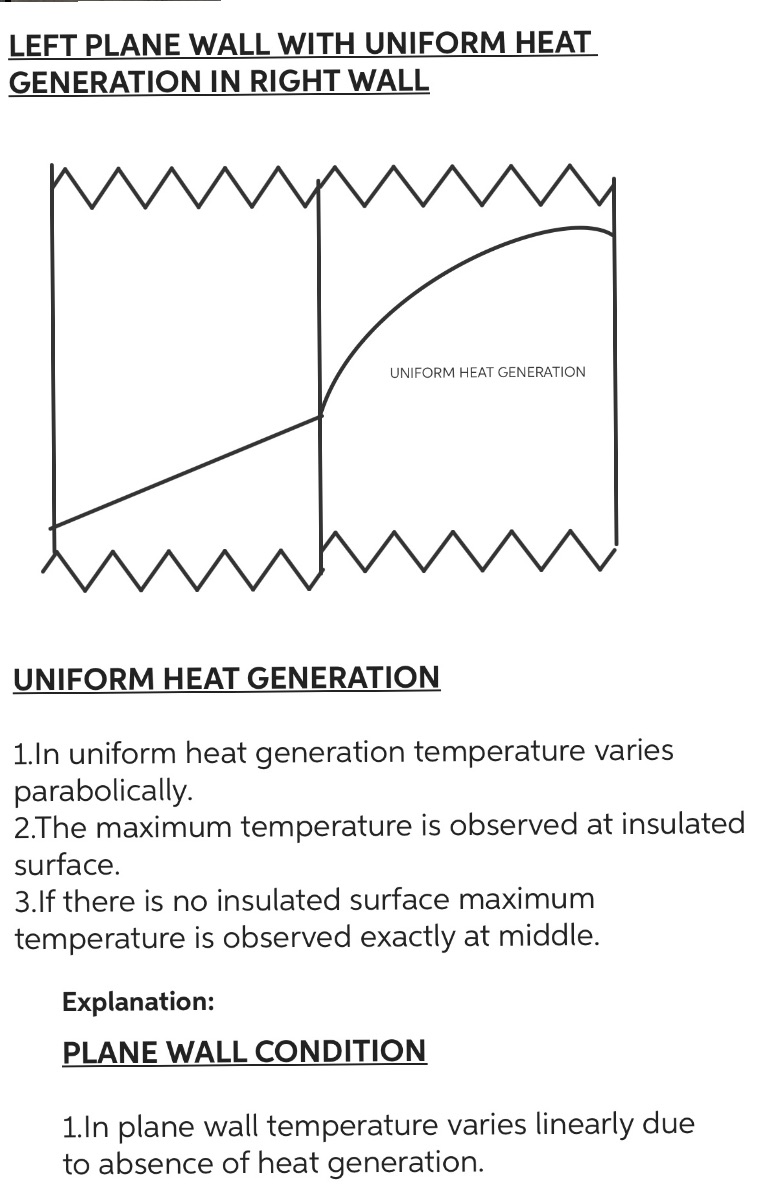
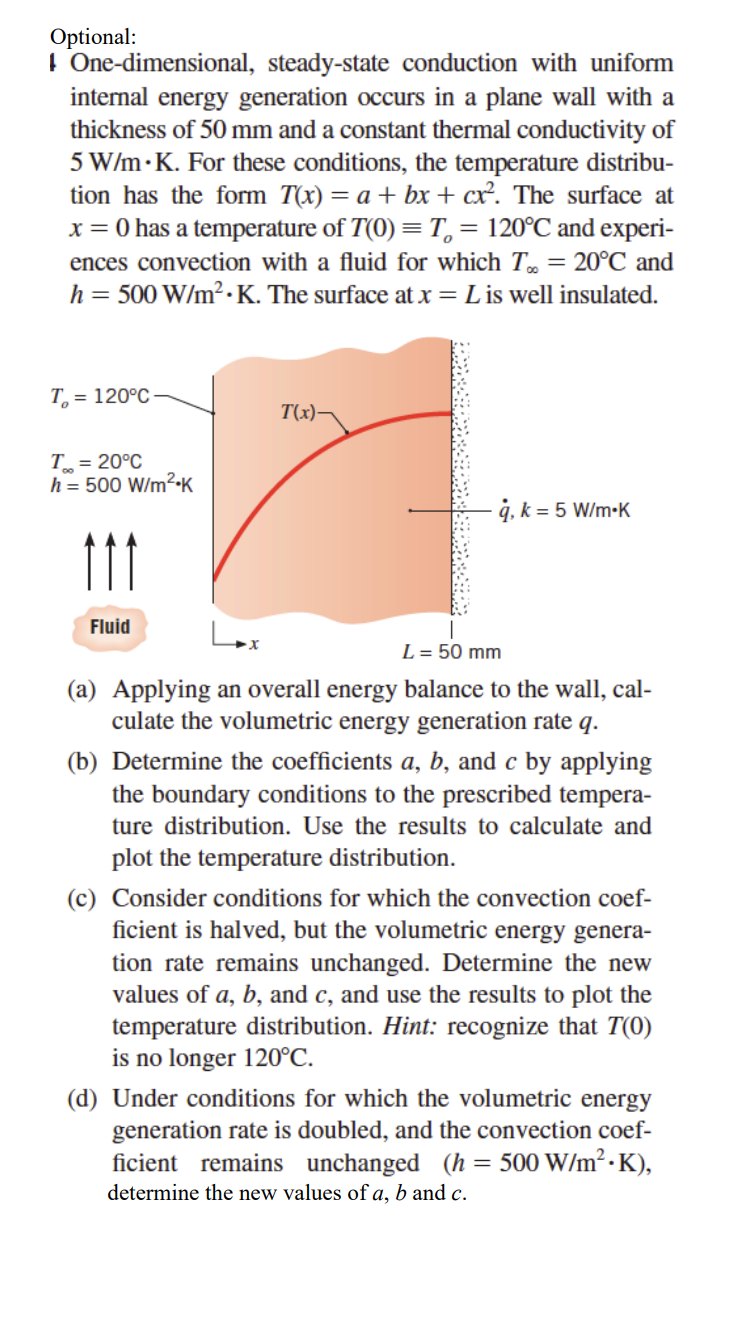
LEFT PLANE WALL WITH UNIFORM HEAT GENERATION IN RIGHT WALL UNIFORM HEAT GENERATION UNIFORM HEAT GENERATION 1.In uniform heat generation temperature varies parabolically. 2.The maximum temperature is observed at insulated surface. 3.If there is no insulated surface maximum temperature is observed exactly at middle. Explanation: PLANE WALL CONDITION 1.In plane wall temperature varies linearly due to absence of heat generation. There is slight modification in solving question Explanation: You have to find interface temperature between two walls,once you get this then you can approach in same way as in the given question to get temperature distribution Let ambient temperature be To and Temperature of left wall be T and Temperature of interface be To 2 500 ert be TL Temperature inter hA(TLT) = q volume Explanation: There are two ways to proceed (we are assuming 1st case) Step 3/3 O 1)either q (volumetric heat generation) is given so we will find TL 2)TL is directly given(this is a easier case) from here you will get T TO FIND TO q x volume = kA(T. - TL) Explanation: generally q is given as heat generation per unit volume.so we multiply it by volume of wall to get total heat. In case width or height or any other dimension of wall not given assume it to be 1 for calculating total volume Optional: One-dimensional, steady-state conduction with uniform internal energy generation occurs in a plane wall with a thickness of 50 mm and a constant thermal conductivity of 5 W/m.K. For these conditions, the temperature distribu- tion has the form T(x) = a + bx + cx. The surface at x = 0 has a temperature of T(0) = T = 120C and experi- ences convection with a fluid for which T = 20C and h = 500 W/m.K. The surface at x = L is well insulated. T = 120C T= 20C h = 500 W/m.K Fluid T(x)- q, k = 5 W/m.K L = 50 mm (a) Applying an overall energy balance to the wall, cal- culate the volumetric energy generation rate q. (b) Determine the coefficients a, b, and c by applying the boundary conditions to the prescribed tempera- ture distribution. Use the results to calculate and plot the temperature distribution. (c) Consider conditions for which the convection coef- ficient is halved, but the volumetric energy genera- tion rate remains unchanged. Determine the new values of a, b, and c, and use the results to plot the temperature distribution. Hint: recognize that T(0) is no longer 120C. (d) Under conditions for which the volumetric energy generation rate is doubled, and the convection coef- ficient remains unchanged (h= 500 W/m.K), determine the new values of a, b and c.