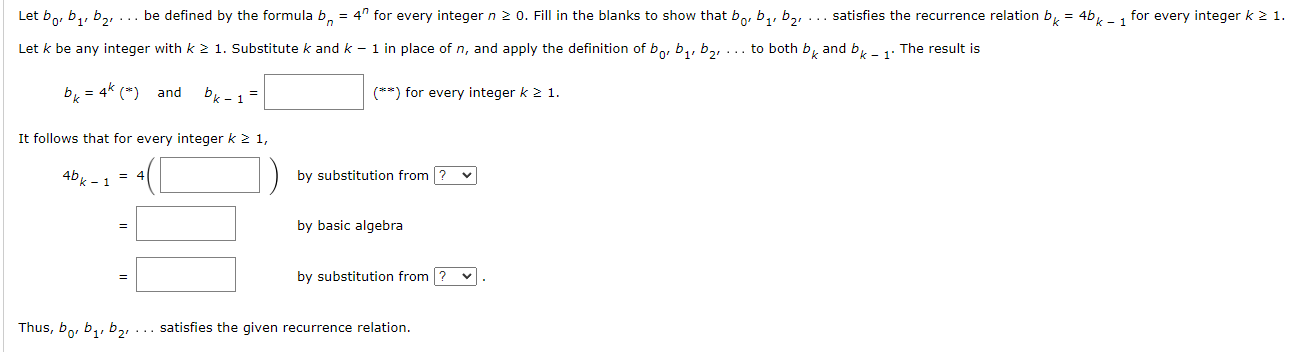
Let bor by, by, . . . be defined by the formula b = 4" for every integer n 2 0. Fill in the blanks to show that bo, by, by, . . . satisfies the recurrence relation by = 4b _ , for every integer k 2 1. Let k be any integer with k 2 1. Substitute k and k - 1 in place of n, and apply the definition of bo, by, by, . . . to both b, and bk _ 1. The result is by = 4k (*) and bk - 1 = (* *) for every integer k 2 1. It follows that for every integer k 2 1, 4bk - 1 = 4 by substitution from |? v by basic algebra = by substitution from ? Thus, bor by, by, . .. satisfies the given recurrence relation