Question: Let C be the parametrizatio y(t) = (cost + tsint, sint - tcost) for t E (0, 00). (a) Use the formula in Q.2 of
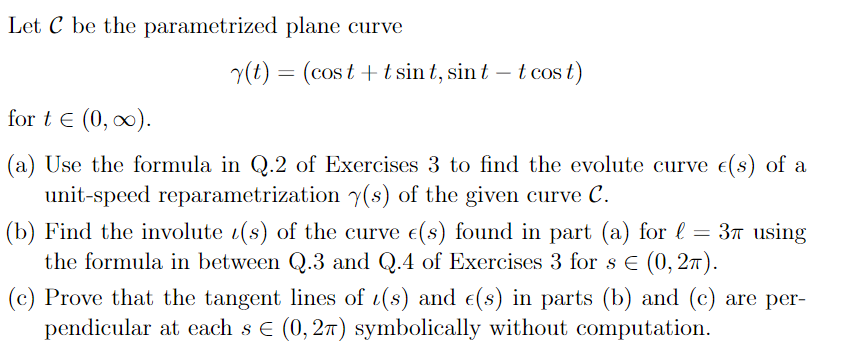



Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


