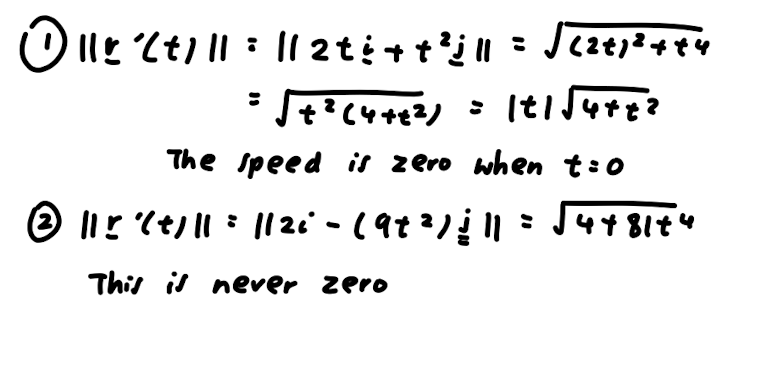
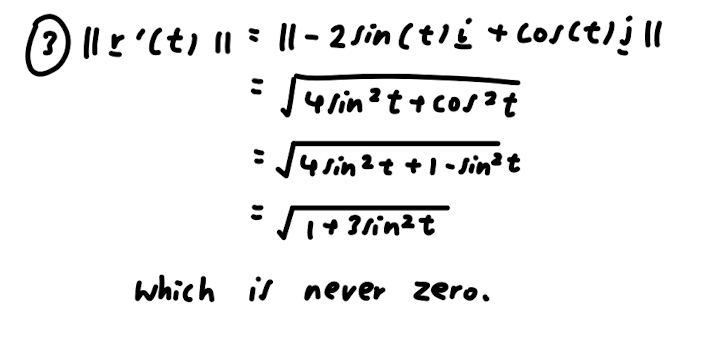
SOLVE BOLDED QUESTION 2a,b,c & 3a,b PLEASE

QUESTION 2

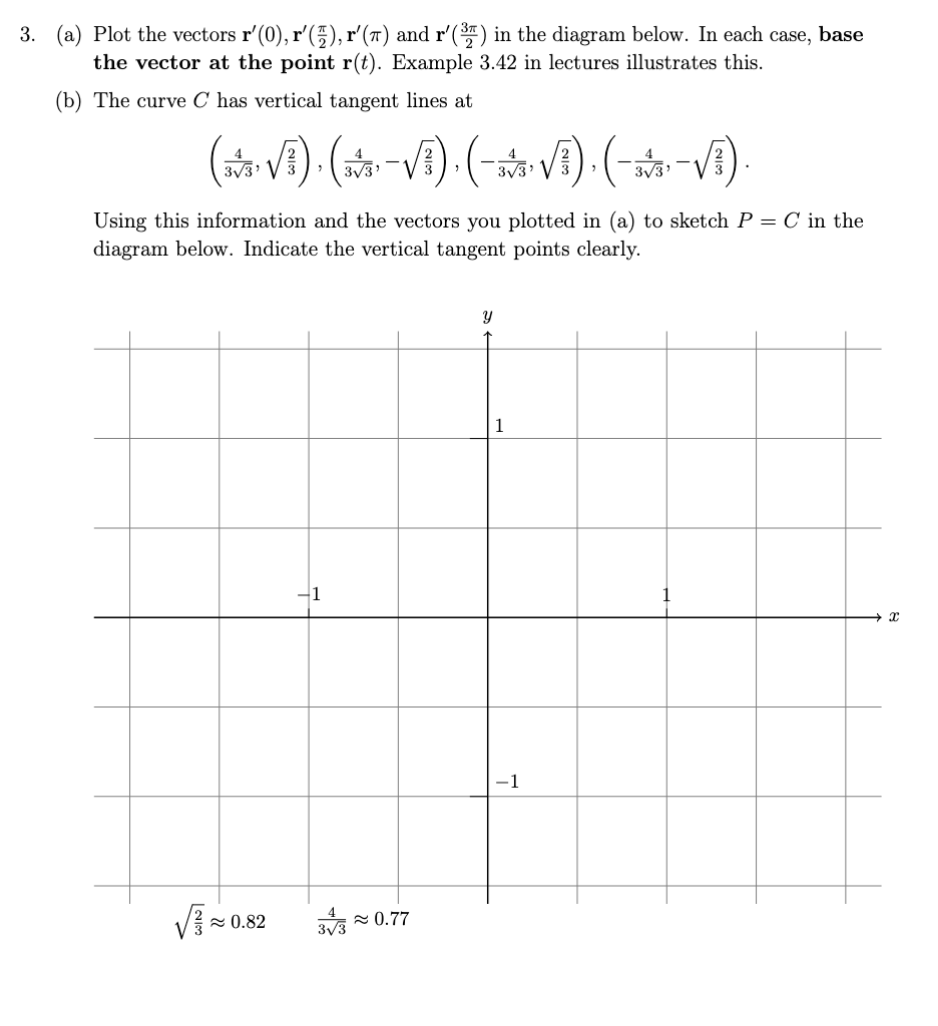
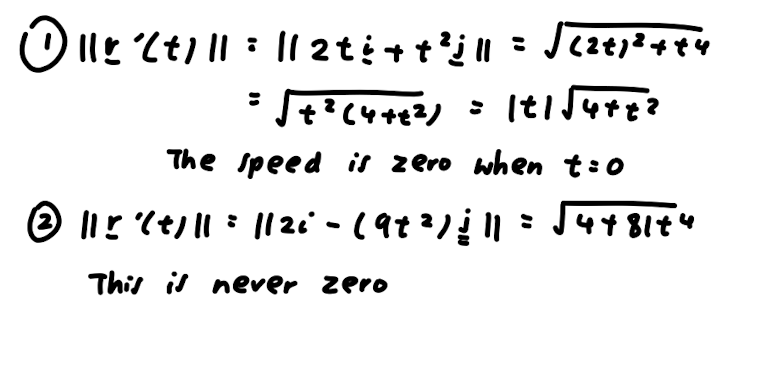
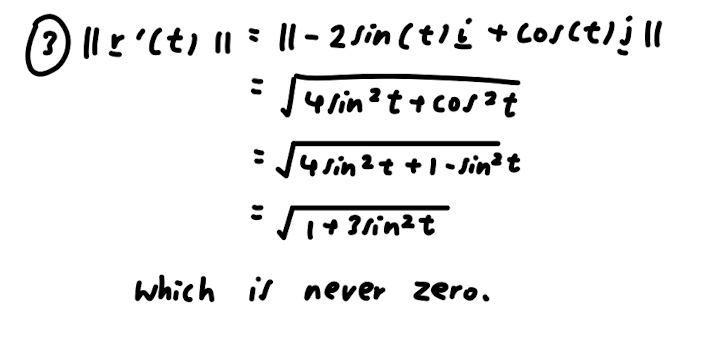
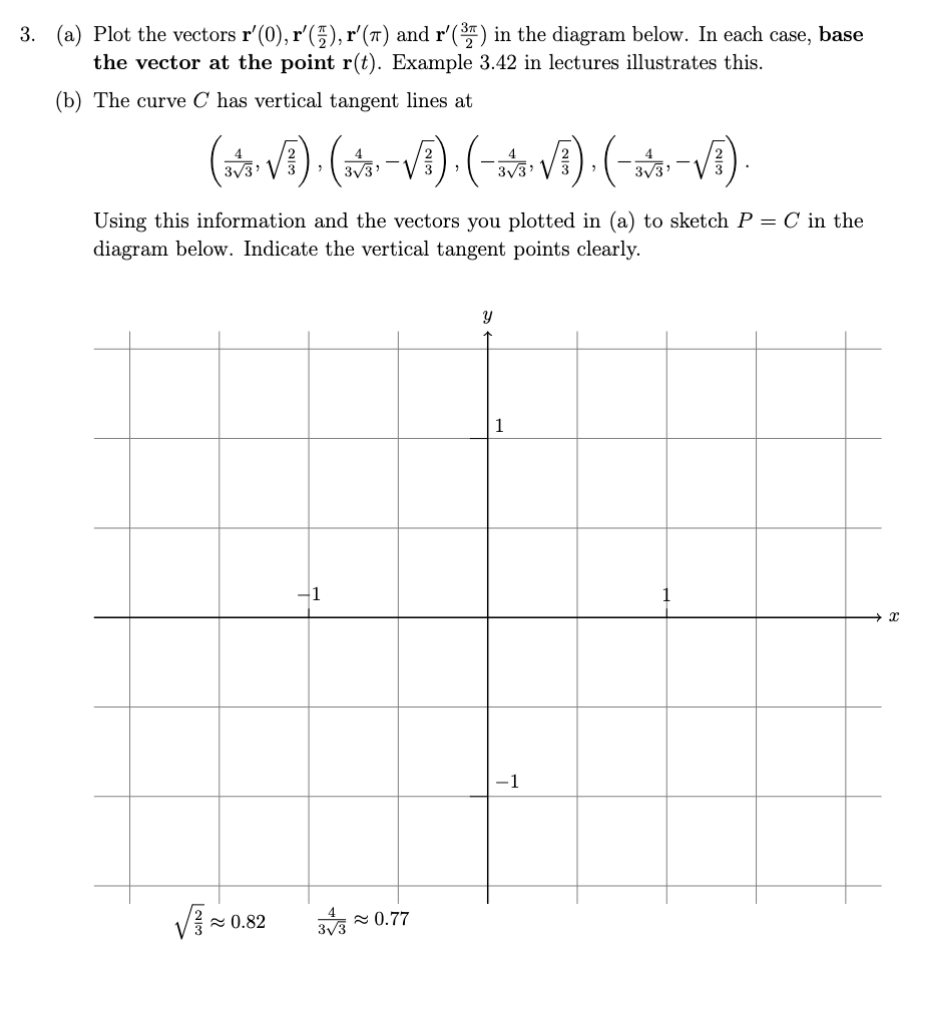
2. Parametric vs Cartesian description. (a) Let (x, y) E P. This means a = cos(t) and y = sin(2t), so: LHS = 4x + y' = 4(cos(t))" + (sin(2t))? = 4 cos* (t) + (2 sin(t) cos(t))2 = 4 cos* (t) + 4sin?(t) cos?(t) = 4 cos (t) (cos? (t) + sin?(t)) = 4 cos'(t) = 4x2 = RHS which shows (x, y) E C. (b) r(#) = 0 and r(# ) = 0. 2 (c) Dividing by 4x2 gives x2 + =1, 80 v = y (d) Let (x, y) E C. If I = 0, equation (1) gives y = 0, so (z, y) = r by (b). If r # 0 then (c) shows ( I, 2 is in the unit circle, so (X, ) = (cos(t), sin(t)) for some te R. This gives I = cos(t) and y = 2 sin(t) cos(t) = sin(2t). Hence (x, y) = r(t), which shows (x, y) E range(r).2. In Questions 2 and 3 we consider the the path P of the parametric curve r : R - R defined by r(t) = 2 cos(t) sin? (t)i + sin(t)j so P = range(r) and the set C = {(x, y) ER? | x2 + 495 = 4y4 }. In Assignment 1, you proved that P C C. Here we use the approach of Question 2 of Practice class 9 (which you should review) to prove that C C P, completing the proof that P = C. (a) Find the x intercept of C (there is only one) and explain why it is in P. (b) Assuming y # 0, rearrange the equation for C into the form u + y? = 1 where u is expressed in terms of x and y. You should give a formula for u. (c) In (b), you showed that (u, y) is in the unit circle. Use this to complete the proof that C C P.3. {3) Plot the vectors r'(),r'(), r'(1r) and t?) in the diagram below. In each case, base the vector at the point r(t). Example 3.42 in lectures illustrates this. (b) The curve C has vertical tangent lines at i 2 i_ 2 _i\\/ _i_ 3 (if! s)'(w's :s)=( w? a ' M) a ' Using this information and the vectors you plotted in (a) to sketch P = C in the diagram below. Indicate the vertical tangent points clearly. 2. Parametric vs Cartesian description. Here we show that the curve C of Question 1 is equal to the path P = range(r) of the curve r : R > R2 dened by r(t) = cos(t)i + sin(2t)j. In other words, we show that P = C. We can then use r' to analyse the behaviour at (U, 0). (a) (b) (C) (d) (6) Show that P Q C using our standard approach to subset proofs. Find g) and r033\"). Assuming a: 75 0, rearrange the equation for G into the form m2+02 = 1 where 'u is an expression in :1: and y. You should give a formula for 1). In part (c), you showed that (any) is in the unit circle (do you see why?). Use this to show that 0 g range(r). That is, show that every solution of the equation for C is of the form :1: = cos(t), y = sin(2t) for some t. Don't forget to discuss the special case :1: = 0. Plot g) and r'(37\") as arrows on your diagram from Question 1. What information does this give about the shape of the curve at (0,0)? Think about our geometric interpretation of the velocity vector. Example 3.42 For each curve, give a formula for the speed at time t: 1. r(t) : (t2 + 1)i + @153 + 1)]. 2. r(t) : 2ti (3t3 + 1)j. 3. r(t) = 2 cos(t)i + sin(t)j. and find any times at which the speed is 0. \fw Il x ' ( t ) n1 : 11 - 2 sin ( tic + cos ct ) ill 4 /in ? t + cos ? t 4 in 2+ + 1 - lin't which is never zero