Question: Let f is a real-valued uniformly continuous function on [0, ). Show that if f is Lebesgue integrable on [0, 0), then lim f(x)

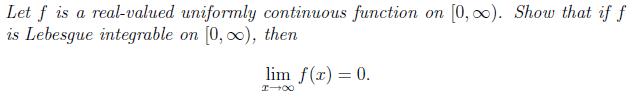
Let f is a real-valued uniformly continuous function on [0, ). Show

Let f is a real-valued uniformly continuous function on [0, ). Show that if f is Lebesgue integrable on [0, 0), then lim f(x) = 0. I-X

Step by Step Solution

★★★★★

3.49 Rating (149 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock

The detailed ... View full answer

blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Q:

Let f be continuous on [a, b] and thus integrable there. Show that f(x) dxsf(x) dx

Q:

Let f be a nonnegative continuous function on [0,1]. (a) Show that (b) Use part (a) to evaluate xf(sin x) dx = (n/2) | f(sin x) dx. x sin x cos x ax.

Q:

Let f be a nonnegative continuous function defined on 0 ( x Show that (a) If limx( f(x) exists it must be 0; (b) It is possible that limx( f(x) does not exist. Roa f(x) dx

Q:

Describe the steps in the new product development process adopted by Company T. Would it be advisable that companies strictly follow these stages? READ: Improving new product development (NPD)...

Q:

1 Back to basics to start this course: Define project. What are the five project process areas - give a short explanation of each. What are the ten project knowledge areas - give a short explanation...

Q:

Let \(f: \mathbb{R} ightarrow \mathbb{R}\) be a bounded increasing function. Show that \(f^{\prime}\) exists Lebesgue a.e. and \(f(b)--f(a) \geqslant \int_{(a, b)} f^{\prime}(x) d x\). When do we...

Q:

Dashboard X | PCRS X ChatGPT X Quiz: Pre-Clas X STA 130 Ment X STA130 1:1 Me X ] Old Exams Re X I+ O X 2 q.utoronto.ca/courses/319691/quizzes/345744/take Relaunch to update : New Tab ACORN Dashboard...

Q:

All questions. 05:50:42 VA; 25% ' ASSIGNMENTNM1.pdf IQ 0+ Numerical Methods-Assignment-l Mathematical Prelimanaries, Taylor's Theorem, Order of Convergence (1) Let L be a real number and let {an} be...

Q:

Handwri.te and show all work and steps 1. Part 1 - Application An airplane is flying on a bearing of 170 at 495 mph. Find the component form of the velocity of the airplane. Be sure to show and...

Q:

Which is not a capability that supports adaptability and resiliency? Question options: A. Organizational relationships with external stakeholders B. Deferring decision making to the last responsible...

Q:

Walt Disney Company (Disney) is a diversified international entertainment company with operations in three business segments. Revenue and operating income data for the three segments are shown below....

Q:

1 . You may purchase a parcel of land for its current market price of $ 6 , 0 0 0 , 0 0 0 . Restrictive covenants only allow you to build a hotel on the land. 2 . The parcel of land is currently...

Q:

Write SQL statement to create a single table for the STAR entity identified in the E-R model you created last week. Then add one or two rows of sample data into the STAR table (feel free to pick your...

Q:

2. If the coordinate frame oixiyizi is obtained from the coordinate frame ooxoyozo by a rotation of /2 about the x-axis followed by a rotation of /2 about the fixed y-axis, find the rotation matrix R...

Q:

In 2 0 2 3 , Sterling and Lana Archer ( ages 3 1 and 2 9 ) are married and live in New York, NY . Their address is 8 8 0 5 th Ave Unit 2 2 A , New York, NY 1 0 0 2 1 . They have a two - year - old...

Q:

Solve the following 1,4 3 2TT 5x- 1+ (15 x) dx 5X

Q:

At December 31, 2016, McKinleys price-earnings ratio was 13.4. For 2016, McKinleys net income was $660,000, its earnings per share was $7.00, and its annual dividend per share was $4.00. What was the...

Q:

MgO prevents premature evaporation of Al in a furnace by maintaining the aluminum as Al2O3. Another type of matrix modifier prevents loss of signal from the atom X that readily forms the molecular...

Q:

An article in Electric Power Systems Research [On the Self-Scheduling of a Power Producer in Uncertain Trading Environments (2008) considered a self-scheduling approach for a power producer. The...

Q:

Construct a 2 III 52 design in eight runs. What are the alias relationships in this design?

Q:

Suppose X and Y are independent continuous random variables. Show that XY = 0.

Q:

The vendor of a residential property accepted a $40,000 take-back mortgage to facilitate the sale. The agreement calls for quarterly payments to amortize the loan over 10 years at an interest rate of...

Q:

A mortgage contract for $45,000 written 10 years ago is just at the end of its second five-year term. The interest rates were 8% com- pounded semiannually for the first term and 7% compounded...

Q:

Even though the borrower will likely pay a higher interest rate upon renewal in one year, assume for the moment that the interest rate and monthly payment will not change. In each case, how long from...