Question: Let f : R - R be a continuous function. Now, define fr : R - R by fn(2) = f(x + 1) Suppose that

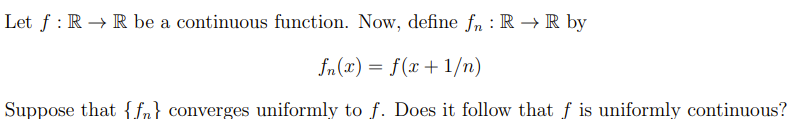
Let f : R - R be a continuous function. Now,

Let f : R - R be a continuous function. Now, define fr : R - R by fn(2) = f(x + 1) Suppose that { f } converges uniformly to f. Does it follow that f is uniformly continuous

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Q:

Question 2. Consider the sequence (a,) given by a; = a, a,+1 = a,(2 a,) for n > 1,where a R. (a) Find all the values of o R such that (a,) converges, and for each of these values of , find the limit...

Q:

1. (1-year) Prove that for every n E N there exists a unique t(n) > 0 such that (t (n) - 1) Int(n) = n. Calculate lim (t(n) Inn ) . 1 - 00 2. (1-year) Let {an, n 2 1} C R be a bounded sequence....

Q:

1. (1-year) Prove that for every n E N there exists a unique t(n) > 0 such that (t (n) - 1) Int(n) = n. Calculate lim (t(n) Inn ) . 1 - 00 2. (1-year) Let {an, n 2 1} C R be a bounded sequence....

Q:

course 2 week 1 If writing process is bothering you, it's ok to write only correct answer in each question. 1. Let f (r, y) be a continuous function of two variables. If you take the definite...

Q:

2. Let g : R - R be a bounded function and define f : R {0} - Rby f (x) = 8(x) +- Using only the definition above, and without using any limit rules, prove that f (x) > two as x - 0

Q:

Hi tutor. Kindly help me solve these I1 Exercise 2. Let f: R" + R be a real-valued function on R", and Xo = E R a In point. (a) If f is differentiable at Xo, explain what it means to say that the...

Q:

[7] Problem 3 Definition: A function f : IR - R is said to vanish at infinity if lim f(x) = lim f(x) =0. I-+ 400 I )-00 (a) Prove that if f : R - R is a continuous function that vanishes at infinity,...

Q:

Plz help me solve the problem. Problem 6. (15 points) (a) (5 points) Let f : (0, 00) > R be the function given by f(:r) = i, for every x G (O, 00). Prove that f is continuous at :r = 1 by using the...

Q:

ACORN Timeout x tut8.pdf: MAT 137Y F/W 2020-20 x [ mat137_hw4.pdf: MAT 137Y F/W x () mat137_hw4 (1).pdf * + X O X1+ | C:/Users/User/Downloads/mat137_hw4%20(1).pdf . . 1 12 - + ment is worth 10...

Q:

ACORN Timeout x tut8.pdf: MAT 137Y F/W 2020-20 x [ mat137_hw4.pdf: MAT 137Y F/W x () mat137_hw4 (1).pdf * + X O X1+ | C:/Users/User/Downloads/mat137_hw4%20(1).pdf . . 1 12 - + ment is worth 10...

Q:

Suppose a certain population of observations is normally distributed. (a) Find the value of z* such that 95% of the observations in the population are between - z* and + z* on the Z scale. (b) Find...

Q:

In three dimensions the equation Question 12 22 + y? = 1 Not yet answered Marked out of 7 represents a Similarly, the equation P Flag question y? +22 = 1 represents another cylinder. These cylinders...

Q:

Anderson international Limited ls eviluating a profect in Eitwhon. The propect wat otite the followhg cenh fowr: \ table [ [ \ table [ [ Thar ] , [ - ] ] , Cant elina ] , [ , - if 5 9 1 , 0 e 9 ] , [...

Q:

please answer only if you know programming language is c++ For this lab, your objective is to define the functions below. Define the void function SwapNodes () that takes three generic type Node...