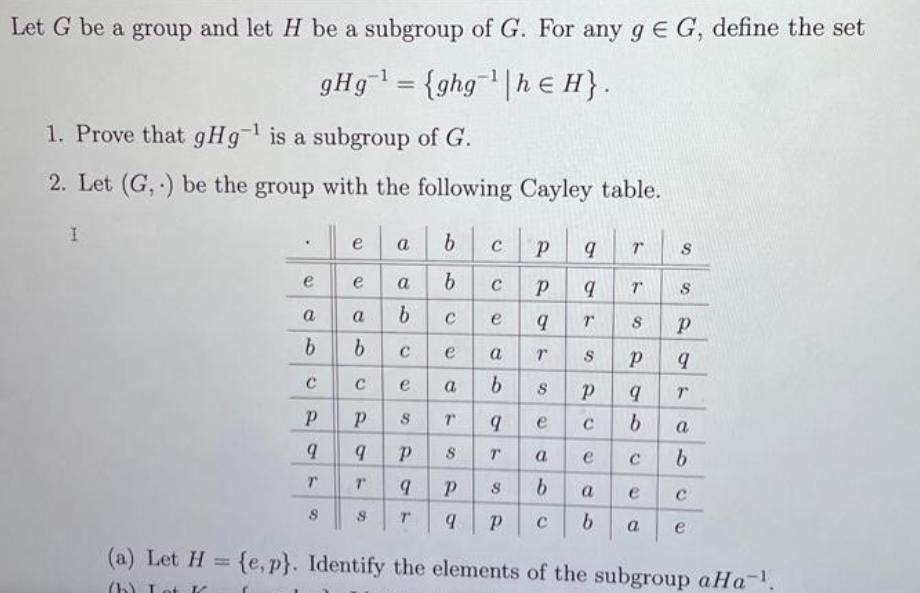
Let G be a group and let H be a subgroup of G. For any g = G, define the set gHg= {ghg|he H}. 1. Prove that gHg is a subgroup of G. 2. Let (G,) be the group with the following Cayley table. I e a b 9 T 8 e e a a b a b C C e 8 9 T b b 8 T e a T 8 9 9 C 9 9 9 T a T b 8 9 e T a C e 8 T T 8 S P P 9 C b S S 9 T a b e bae C b a e (a) Let H = {e, p}. Identify the elements of the subgroup aHa-. (b). Lot K