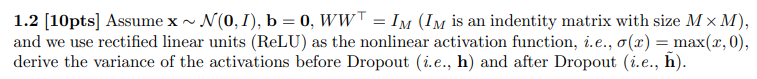
Let us consider a single hidden layer MLP with M hidden units. Suppose the input vector xRN1. The hidden activations hRM1 are computed as follows, h=(Wx+b) where weight matrix WRMN, bias vector bRM1, and is the nonlinear activation function. Dropout [1] is a technique to help reduce overfitting for neural networks. In PyTorch, Dropout is implemented as follows. During training, we independently zero out elements of h with probability p and then rescale it with 1p1, i.e., h~m[i]=1pmhBernoulli(1p)i=1,,M, where is the Hadamard product (a.k.a., element-wise product) and Bernoulli (1p) is the Bernoulli distribution where the random variable takes the value 1 with the probability 1p. During testing, we just use h~=h. 1.2[10pts] Assume xN(0,I),b=0,WW=IM(IM is an indentity matrix with size MM), and we use rectified linear units (ReLU) as the nonlinear activation function, i.e., (x)=max(x,0), derive the variance of the activations before Dropout (i.e., h) and after Dropout (i.e., h~)