Let X and Y be as in the triangle example in Exercise 9.15. Recall from

Exercise 9.16 that X and Y represent the minimum and maximum coordinate

of a point that is drawn from the unit square: X = min{U, V } and Y =

max{U, V }.

a. Show that E[X]=1/3, Var(X)=1/18, E[Y ]=2/3, and Var(Y )=1/18.

Hint: you might consult Exercise 8.15.

b. Check that Var(X + Y )=1/6, by using that U and V are independent

and that X + Y = U + V .

c. Determine the covariance Cov(X, Y ) using the results from a and b.

10.14 Let X and Y be two random variables and let r, s, t, and u be

arbitrary real numbers.

a. Derive from the definition that Cov(X + s, Y + u) = Cov(X, Y ).

b. Derive from the definition that Cov(rX, tY ) = rtCov(X, Y ).

c. Combine parts a and b to show Cov(rX + s, tY + u) = rtCov(X, Y ).

The mean number of customers appearing in a bank during a self-assertively picked hour is four. The bank boss is contemplating reducing the amount of tellers. however, she should be sure that lines don't get unreasonably long. She infers that if near two customers come in during a 15-minute stretch of time. two tellers (instead of the current three) will be sufficient. a What is the probability near two customers will come in the bank during an indiscriminately picked 15-minute time span? b What is the probability that different customers will come in during two consecutive 15-minute intervals of time? c The director records the amount of customers coming in during 15-minute time frames until she sees a time interval during which various customers appear. Eight time periods have been recorded, each with two or less customers appearing in each. What is the probability that more than 14 time periods will be seen before having different customers appearing during an organized 15-minute term.

Question 66

A particular sort of microorganisms cell detaches at a reliable rate An as time goes on. Thusly, the probability that a particular cell will segregate in a little interval of time t is generally At. Given that a general population starts at time zero with k cells of this sort, and cell divisions are self-ruling of one another, the size of the general population at time t, X (t), has the probability spread

(t) = it] = (11 - I ) e-Akt k - 1

1 _ e-ity-k

71 =

a Find the ordinary worth of X (t) to the extent An and t. b If, for a particular kind of microorganisms cell, A = 0.1 each second, and the general population starts with two cells at time zero, find the typical people size following 5 seconds.

Question 67

During World War I, the British government set up the Industrial Fatigue Research Board (IFRB), later known as the Industrial Health Research Board (IHRB) (Haight 2001). The board was made because of stress for the tremendous number of accidental passings and wounds in the British clash creation undertakings. One of the enlightening lists they considered was the amount of setbacks experienced by women managing 6-inch shells during the period February 13, 1918 to March 20, 1918. These are appeared in the table that follows. Subsequently, 447 women had no accidents during this time span. regardless, 2 had in any occasion 5 setbacks. Number of Frequency Accidents Observed

0 447 1 132 2 42 3 4 3 5 or more a Find the ordinary number of accidents a woman had during this time period. (Anticipate that all discernments in the characterization - at any rate 5" are really 5.)

b After created by von Bortkiewicz (see Section 4.7.3), the Poisson movement had been applied to innumerable self-assertive miracles and, with few uncommon cases, had been found to portray the data well. This had driven the Poisson allocation to be known as the 'unpredictable dissemination," a term that is at this point found in the composition. Along these lines, the mathematicians at the IFRB began by showing these data using the Poisson movement. Find the typical number of women having 0, 1, 2, 3, 4, and 5 incidents using the mean found somewhat (a) and the Poisson scattering. How well do you think this model portrays the data?

c Greenwood and Woods (1919) prescribed fitting a negative binomial assignment to these data. Find the typical number of approved drivers having 0,1, 2, 3, 4, and 5 setbacks using the mean found in part (a) and the numerical (negative binomial with r= 1) dispersal. How well do you think this model depicts the data? Credible note: Researchers were puzzled with respect to why the negative binomial fit better contrasted with the Poisson appointment until, in 1920, Greenwood and Yule proposed the going with model. Expect that the probability any given approved driver will have a setback is passed on by a Poisson scattering with mean A. Nevertheless, A vacillates starting with one woman then onto the next as demonstrated by a gamma transport (see Chapter 5). By then the amount of disasters would have a negative binomial apportionment. The value of A related with an approved driver was called their - disaster tendency."

Question 68

In the game Lotto 6-49, six numbers are discretionarily picked without replacement from 1 to 49. A player who organizes with all of the six numbers in any solicitation wins the large stake.

a What is the probability of winning any given gold mine with one game ticket? b If a game ticket costs $1.00, what are the for the most part expected prizes from playing Lotto 6-49 once. c Suppose an individual gets one Lotto 6-49 ticket each week for seemingly forever. Expecting all years have 52 weeks, what is the probability of prevailing in any event one treasure trove during this time? (Hint: Use a Poisson surmise.) d Given the setting halfway (c), what are the for the most part expected rewards over 100 years?

Question 69

The probability of a customer's appearance up at a fundamental food thing organization counter in any one second reciprocals 0.1. Expect that customers appear in a discretionary stream and, along these lines, that the arrival in any one second is self-sufficient of some other appearance. In like manner acknowledge that at most one customer can appear during any one second.

a Find the probability that the essential appearance will occur during the third 1-second range. b Find the probability that the fundamental appearance will not occur until in any occasion the third 1-second stretch. c Find the probability that no appearances will occur in the underlying 5 seconds. d Find the probability that in any occasion three people will appear in the underlying 5 seconds.

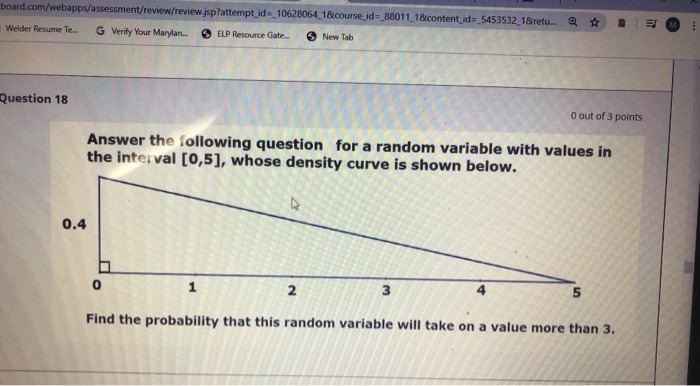
Exercise 4.14. The lifetime of a lightbulb can be modeled with an exponential random variable with an expected lifetime of 1000 days. (a) Find the probability that the lightbulb will function for more than 2000 days. (b) Find the probability that the lightbulb will function for more than 2000 days, given that it is still functional after 500 days.board.com/webapps/assessment/review/review.jsp?attempt_id=_10628064_1&course_id=_88011_1&content id=_5453532_1&retu.. 2 M Welder Resume Te... G Verify Your Marylan. (3) ELP Resource Gate.. ) New Tab Question 18 0 out of 3 points Answer the following question for a random variable with values in the interval [0,5], whose density curve is shown below. 0.4 0 2 3 4 Find the probability that this random variable will take on a value more than 3.Suppose that the miles-per-gallon (mpg) rating of passenger cars is a normally distributed random variable with a. mean and a standard deviation of 33.8 and 3.5 mpg, respectively. a. What is the probability that a randomly selected passenger car gets more than 35 mpg? b. What is the probability that the average mpg of four randomly selected passenger cars is more than 35 mpg? C. If four passenger cars are randomly selected, what is the probability that all of the passenger cars get more than 35 mpg