Likelihood ratio

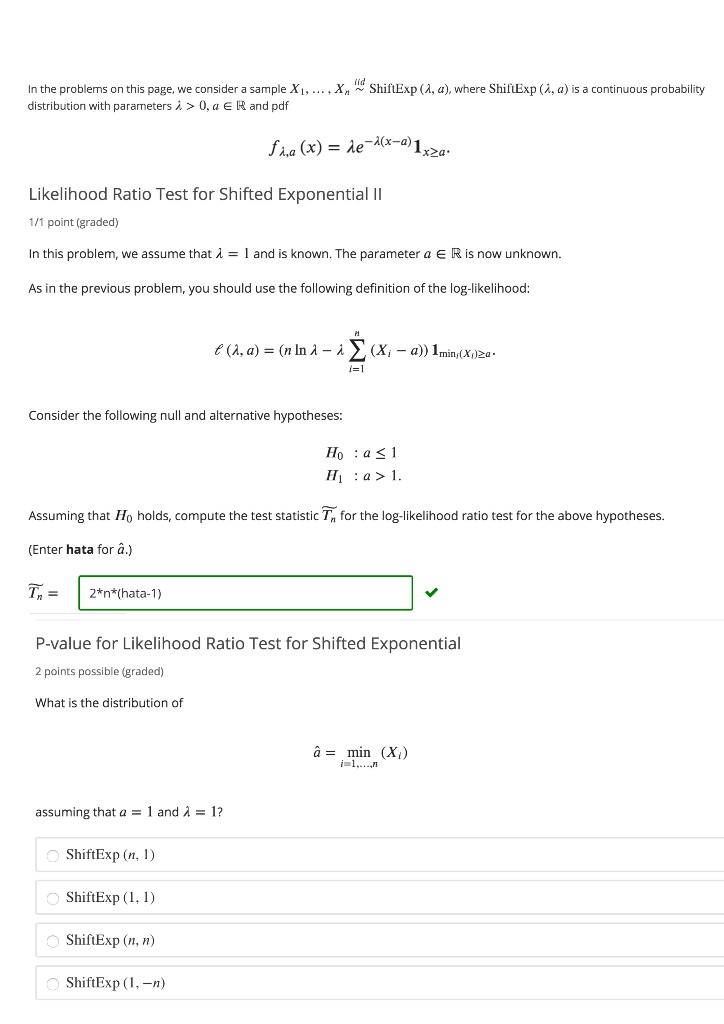
In the problems on this page, we consider a sample X1, .... X, ~ ShiftExp (1, a), where ShiftExp (1, a) is a continuous probability distribution with parameters > > 0, a E I and pdf faa (x) = de-1(x-@)1xza. Likelihood Ratio Test for Shifted Exponential II 1/1 point (graded) In this problem, we assume that 1 = 1 and is known. The parameter a E R is now unknown. As in the previous problem, you should use the following definition of the log-likelihood: f (1, a) = (nina - A > (X; - a)) 1min (X,)24- 1= 1 Consider the following null and alternative hypotheses: Ho : as1 H1 :a>1. Assuming that Ho holds, compute the test statistic 7, for the log-likelihood ratio test for the above hypotheses. (Enter hata for a.) In = 2*n*(hata-1) P-value for Likelihood Ratio Test for Shifted Exponential 2 points possible (graded) What is the distribution of a = min (X/) 1 1.....7 assuming that a = 1 and 1 = 1? ShiftExp (n, 1) O ShiftExp (1, 1) O ShiftExp (n, n) O ShiftExp (1, -m)