Linear Algebra

Final answer only - No Explanation

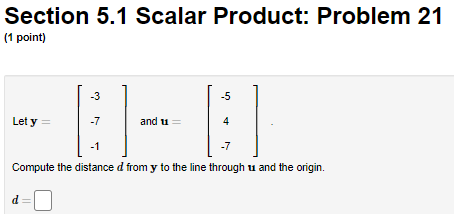
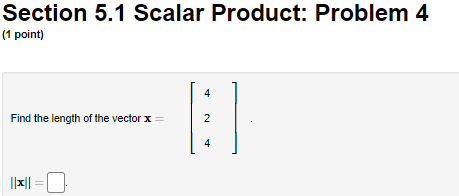
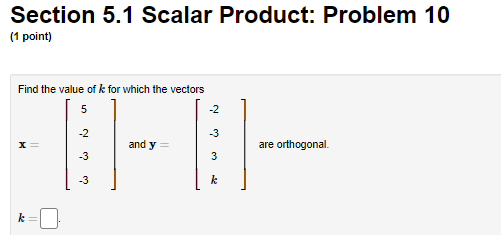
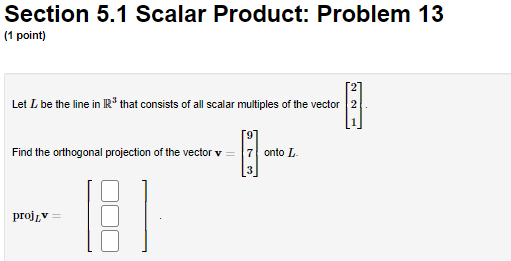
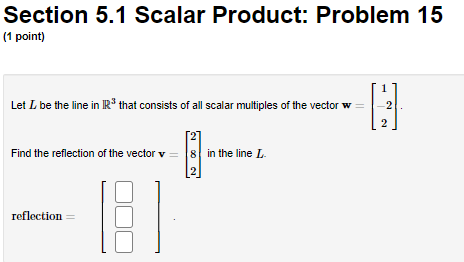
Section 5.1 Scalar Product: Problem 1 [1 point: I 6 Let x a nd 3r -3 III Find the scalar product of I and 3' I"? |:|- Section 5.1 Scalar Product: Problem 10 (1 point) Find the value of & for which the vectors 5 -2 -2 -3 K = and y = are orthogonal. -3 3 -3 k k =Section 5.1 Scalar Product: Problem 11 (1 point) Find a non-zero vector & perpendicular to the vectors 1 = and 2Section 5.1 Scalar Product: Problem 12 (1 point) Find two linearly independent vectors perpendicular to the vector D = 7Section 5.1 Scalar Product: Problem 13 [1 point: 2 Lei L be the line in \"23 thal consists of all scalar multiples of the vector [ 1 1 [I Find the orthogonal projection oi the vector v [T] onlo L :5 I; pmj I." |_| |:| Section 5.1 Scalar Product: Problem 14 (1 point) Find the scalar and vector projection of the vector b = (-3, -4, -1) onto the vector a = (3,5, -2). Scalar projection (i.e., component): Vector projectionSection 5.1 Scalar Product: Problem 15 (1 point) Let [ be the line in IR" that consists of all scalar multiples of the vector w= 2 2 Find the reflection of the vector v = in the line L 2 reflection =Section 5.1 Scalar Product: Problem 16 (1 point) Find the point on the line y = 6x that is closest to the point P = (6,3). Point=Section 5.1 Scalar Product: Problem 17 (1 point) Find an equation of the plane through the point (5, -5, 4) and perpendicular to the vector (3, -1, -2). Do this problem in the standard way or WebWork may not recognize a correct answer.Section 5.1 Scalar Product: Problem 18 1 point) Find the distance from the point Q = (-3,5, -4) to the plane : - 4y - 2: = 7.Section 5.1 Scalar Product: Problem 19 (1 point) Find the distance from the point (6, 3) to the line 31 - 4y = 0. Distance =Section 5.1 Scalar Product: Problem 2 [1 point: -3 -3 Let x -1 and y -4 4 -4 Find the scalar product of I and 3' 1T; |:|. Section 5.1 Scalar Product: Problem 20 (1 point) Find the point on the line y = 3x + 1 that is closest to the point (4, 1) . Point =Section 5.1 Scalar Product: Problem 21 (1 point) -5 and 11 = A Let y = -7 7 Compute the distance d from y to the line through u and the origin.Section 5.1 Scalar Product: Problem 3 (1 point) -3 Find the norm of the vector x= -9Section 5.1 Scalar Product: Problem 4 (1 point) 4 Find the length of the vector x = 2 4Section 5.1 Scalar Product: Problem 5 (1 point) Let {el, 02, es, en es, es} be the standard basis in IR". Find the length of the vector x = 5e, + 5ez + 3es + 5e, + 3es + 206. =Section 5.1 Scalar Product: Problem 6 (1 point) Let X= Find the norm of x and the unit vector in the direction of x. 11 =Section 5.1 Scalar Product: Problem 7 (1 point) Find the angle d between the vectors -4 4 -2 and b = 3 5 (radians).Section 5.1 Scalar Product: Problem 8 (1 point) Find the angle a between the vectors -3 5 and -1 Enter your answer in radians.Section 5.1 Scalar Product: Problem 9 (1 point) Find a non-zero vector 1 perpendicular to the vector it =