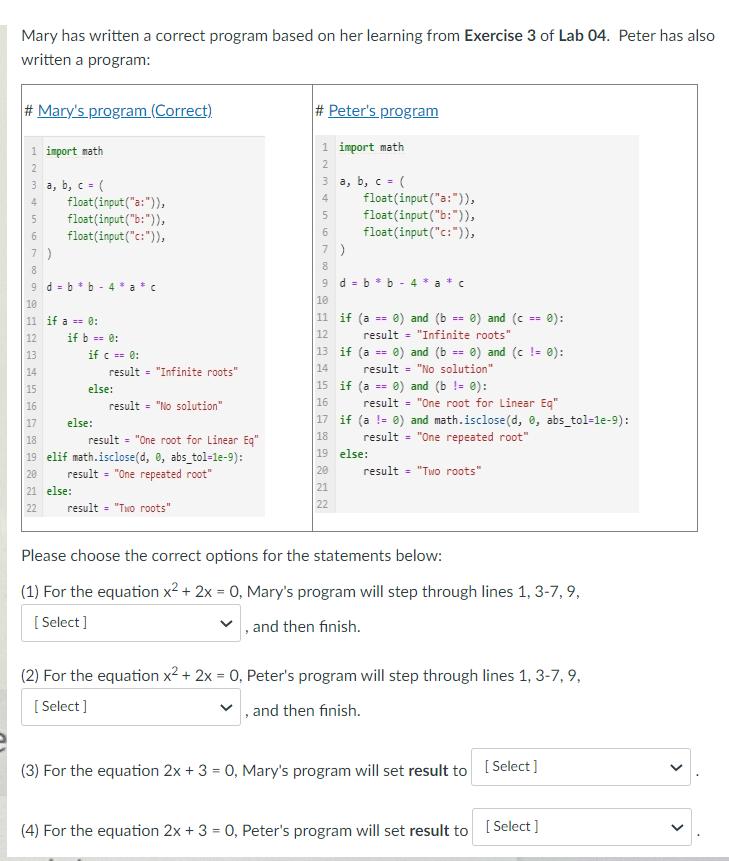
Mary has written a correct program based on her learning from Exercise 3 of Lab 04. Peter has also written a program: # Mary's program (Correct) 1 import math 2 3 a, b, c = ( 4 float(input("a:")), 5 float(input("b:")), 6 float(input("c:")), 7) 8 9 dbb-4 10 11 if a == 0: if b == 0: 12 13 14 15 16 17 18 result = "One root for Linear Eq" 19 elif math.isclose(d, 0, abs_tol-1e-9): 20 result "One repeated root" 21 else: 22 result = "Two roots" if c == 0: result = "Infinite roots" else: else: result = "No solution" # Peter's program 1 import math 7868WNH 2 3 a, b, c = ( 9 d = b 10 float (input ("a:")), float (input("b:")), float (input ("c:")), == 11 if (a == 0) and (b == 0) and (c) result = "Infinite roots" 12 13 if (a == 0) and (b== 0) and (c != 0): 14 result = "No solution" 15 if (a == - 0) and (b != 0): 16 89822 b-4 a c 20 17 if (a != 0) and math.isclose(d, 0, abs_tol-1e-9): 18 result = "One repeated root" 19 else: 21 result = "One root for Linear Eq" 0): result "Two roots" Please choose the correct options for the statements below: (1) For the equation x + 2x = 0, Mary's program will step through lines 1, 3-7, 9, [Select] , and then finish. (2) For the equation x + 2x = 0, Peter's program will step through lines 1, 3-7,9, [Select] , and then finish. (3) For the equation 2x + 3 = 0, Mary's program will set result to [Select] (4) For the equation 2x + 3 = 0, Peter's program will set result to [Select] (1) Options: a11,12,13,19,22 b. 11,19, 22 (2) Options: a. 11,13,15,17,20 b. 17,20 (3) Options: a. infinite roots b. No solution c. One repeated root d. One root for Linear Eq e. Two roots (4) Options: a. Two roots b. One repeated roots