MATHEMATICA GRAPH HELP

Can someone help me with mathematica code to reproduce this graphic... Thanks.

Taken from the article "Thermodynamics of Rubber Elasticity" by J. Pellicer,* J. A. Manzanares, J. Ziga, and P. Utrillas (2001)

HINT

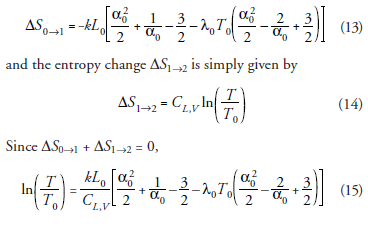
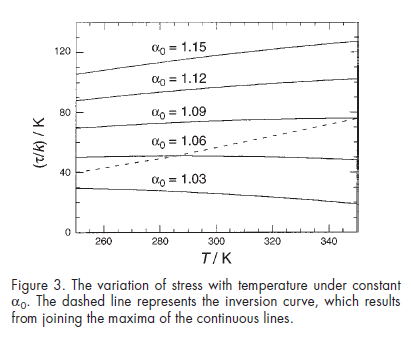
0-1.15 .-1.12 0-1.09 120 80 1.06-- 40 00 1.03 280 TI 260 300 320 340 T/K e variation of stress with temperature under constant Figure 3. Th . The dashed line represents the inversion curve, which results Temperature Changes in Adiabatic Stretching The entropy S of a rubber band at constant volume can be evaluated, by using cq 1 and Maxwell's relation (asaLhy= (at/aT)L,v, as as (10) L 2L where So(T)-S(T,Lo) denotes the entropy in the absence of stress. Figure 4 represents the entropy of rubber 2.2x 104 K-1) at 25 and that of an ideal clastomer (Ao 0) under thc samc conditions. In the case of small strains and for the ideal elastomer, the entropy reduces to which has also been represented in Figure 4 The decrease of S with L at constant Tand Vhas somc interesting implications for the changes observed in tempera- ture when the length of the rubber band is varicd under adia batic (and constant volume) conditions. By using the Maxwell relation (a Tal)sv (at/as)LM the derivative (a T7aL)svcan be written as dT OL (12) , 13 2.3 and the entropy change 5-2 is simply given by (14) (15) 0-1.15 .-1.12 0-1.09 120 80 1.06-- 40 00 1.03 280 TI 260 300 320 340 T/K e variation of stress with temperature under constant Figure 3. Th . The dashed line represents the inversion curve, which results Temperature Changes in Adiabatic Stretching The entropy S of a rubber band at constant volume can be evaluated, by using cq 1 and Maxwell's relation (asaLhy= (at/aT)L,v, as as (10) L 2L where So(T)-S(T,Lo) denotes the entropy in the absence of stress. Figure 4 represents the entropy of rubber 2.2x 104 K-1) at 25 and that of an ideal clastomer (Ao 0) under thc samc conditions. In the case of small strains and for the ideal elastomer, the entropy reduces to which has also been represented in Figure 4 The decrease of S with L at constant Tand Vhas somc interesting implications for the changes observed in tempera- ture when the length of the rubber band is varicd under adia batic (and constant volume) conditions. By using the Maxwell relation (a Tal)sv (at/as)LM the derivative (a T7aL)svcan be written as dT OL (12) , 13 2.3 and the entropy change 5-2 is simply given by (14) (15)