MATLAB, and example 2 is attached

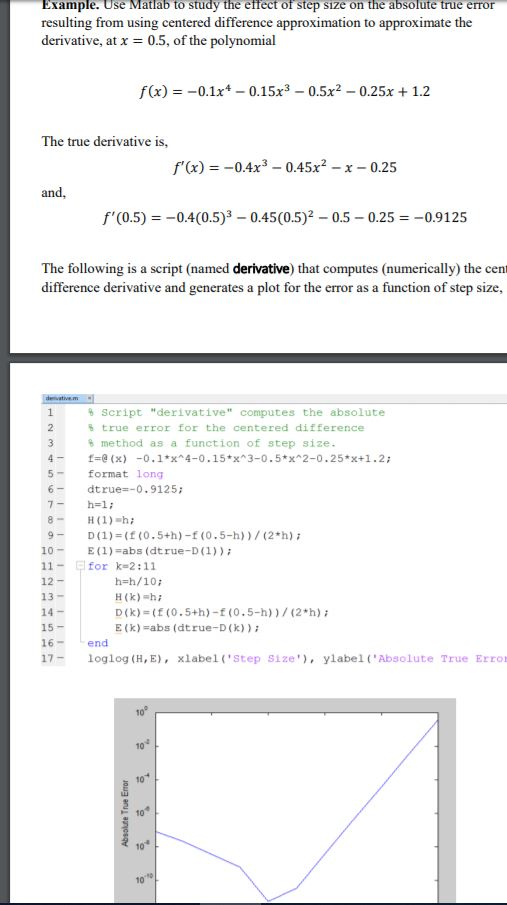
Example. Use Matlab to study the effect of step size on the absolute true error resulting from using centered difference approximation to approximate the derivative, at x0.5, of the polynomial f(x)0.1x 0.15x30.5x2 -0.25x 1.2 The true derivative is, f'(x)--0-4x3-0.45x2--0.25 and, f'(0.5)-0.4(0.5)8- 0.45(0.5)2 0.5 0.250.9125 The following is a script (named derivative) that computes (numerically) the cent difference derivative and generates a plot for the error as a function of step size, % script "derivative" computes the absolute true error for the centered difference method as a function of step size 4- (x)-0.14-0.15*3-0.5*x 2-0.25 x+1.2; 5format long 6- dtrue=-0.9125; 7-h-l: 8-H (1) h 9-D(1) (f (0.5+h)-f (0.5-h))/(2 h)i 10- 11- 12 E( 1 =abs ( dt rue-D ( 1) ) ; for k-2:11 h-h/10 14- 15 D(k) (f (0.5+h)-f (0.5-h) (2 h)i E (k) abs (dtrue-D(k)) 16end loglog (H,E), xlabel ('Step Size), ylabel ('Absolute True Erro 10 10 10 10 Example. Use Matlab to study the effect of step size on the absolute true error resulting from using centered difference approximation to approximate the derivative, at x0.5, of the polynomial f(x)0.1x 0.15x30.5x2 -0.25x 1.2 The true derivative is, f'(x)--0-4x3-0.45x2--0.25 and, f'(0.5)-0.4(0.5)8- 0.45(0.5)2 0.5 0.250.9125 The following is a script (named derivative) that computes (numerically) the cent difference derivative and generates a plot for the error as a function of step size, % script "derivative" computes the absolute true error for the centered difference method as a function of step size 4- (x)-0.14-0.15*3-0.5*x 2-0.25 x+1.2; 5format long 6- dtrue=-0.9125; 7-h-l: 8-H (1) h 9-D(1) (f (0.5+h)-f (0.5-h))/(2 h)i 10- 11- 12 E( 1 =abs ( dt rue-D ( 1) ) ; for k-2:11 h-h/10 14- 15 D(k) (f (0.5+h)-f (0.5-h) (2 h)i E (k) abs (dtrue-D(k)) 16end loglog (H,E), xlabel ('Step Size), ylabel ('Absolute True Erro 10 10 10 10