matlab code

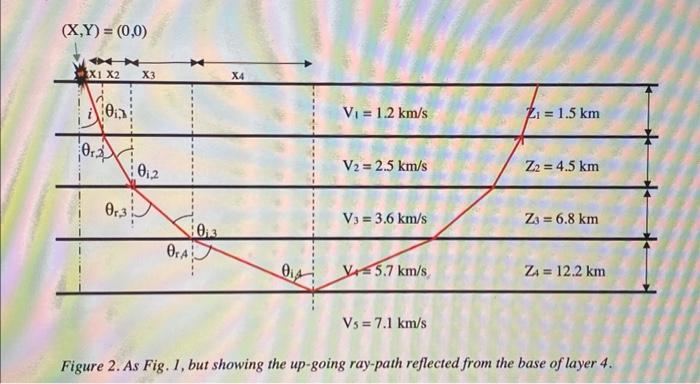
(XY)=() V5=7.1km/s Figure 1. Schematic ray-path for propagation in layered media. Cartesian co-ordinate system (X,Y). The source is at the origin (0,0). xn is the distance the ray has travelled in direction X in the n th layer. Vn is the velocity of the nth layer. Zn is the thickness of the nth layer. The takeoff angle is i. The incidence angles at the base of the nth layer is i,n. The refraction angles for the ray entering the nth layer are r,n. 1. Calculate the ray-paths for a takeoff angle of 10 degrees using the model in Fig. 1 (use your script/functions from last week's practical and modify the velocity and depth model). Use matlab to plot the ray paths, indicating the layer boundaries, copy the figure into a word document (label Figure 1) and add a caption. Describe the process of refraction, referring to the figure (or figures). (10 marks) 2. In this model (Fig. 1), with a take-off angle of 10 degrees, total internal reflection occurs at the base of the fourth layer. Extend your script to calculate the ray-paths for the upgoing wave. Use matlab to plot the ray path for the wave reflected from the base of layer 4 , from source back to the surface (e.g., Fig. 2), indicating the layer boundaries. Copy the figure into your word file and add a caption, describing the elements of the figure. Submit commented code (not the workspace) (save it as q2m and add any relevant function files) and Figure 2 with caption in your word file. What can you say about the up-going ray-path with regards to the down-going path? (20 marks). Figure 2. As Fig. 1, but showing the up-going ray-path reflected from the base of layer 4