MATLAB PROGRAMMING help! Please provide the CODE.

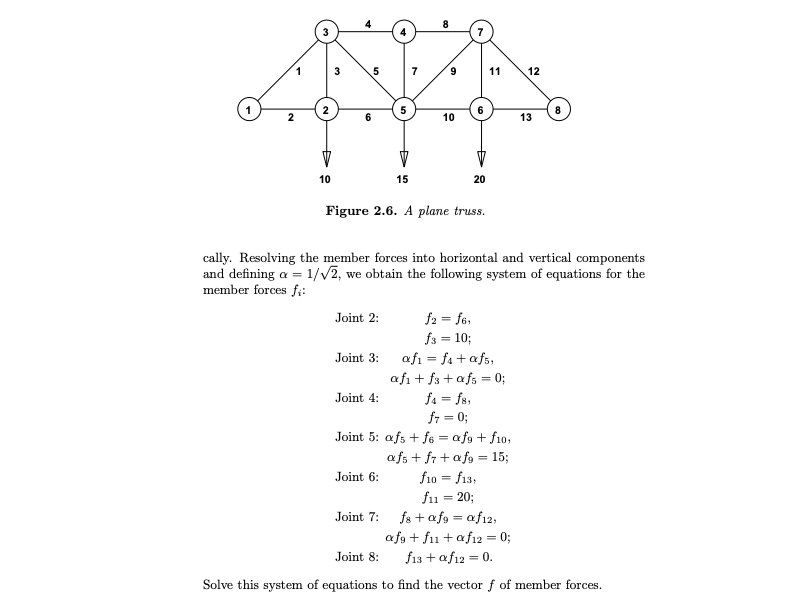
2.3. Figure 2.6 depicts a plane truss having 13 members (the numbered lines) connecting 8 joints (the numbered circles). The indicated loads, in tons, are applied at joints 2, 5, and 6, and we want to determine the resulting force on each member of the truss. For the truss to be in static equilibrium, there must be no net force, hor- izontally or vertically, at any joint. Thus, we can determine the member forces by equating the horizontal forces to the left and right at each joint, and similarly equating the vertical forces upward and downward at each joint. For the eight joints, this would give 16 equations, which is more than the 13 unknown factors to be determined. For the truss to be statically determi- nate, that is, for there to be a unique solution, we assume that joint 1 is rigidly fixed both horizontally and vertically and that joint 8 is fixed verti- 5 7 9 11 12 2 5 6 8 2 6 10 13 10 15 20 Figure 2.6. A plane truss. cally. Resolving the member forces into horizontal and vertical components and defining a = 1/V2, we obtain the following system of equations for the member forces fi Joint 2: f2 = fa. f3 = 10: Joint 3: af1 = fu+afs, afi+f3+afs = 0; Joint 4: f4 = fa. fr = 0; Joint 5: afs + fe = afg+f10; afs+f7+ a fg = 15; Joint 6: f10 = $13, fu = 20; Joint 7: fs + afg = af12, afg+ fui + a f12 = 0; Joint 8: f13+ af12 = 0. Solve this system of equations to find the vector f of member forces