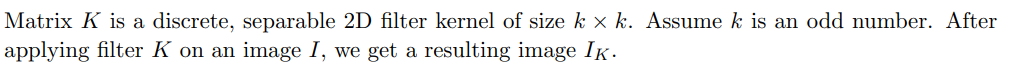
Matrix K is a discrete, separable 2D filter kernel of size kk. Assume k is an odd number. After applying filter K on an image I, we get a resulting image IK. (a) (3 points) Given an image point (x,y), find its value in the resulting image, IK(x,y). Express your answer in terms of I,k,K,x and y. You don't need to consider the case when (x,y) is near the image boundary. (b) (5 points) One property of this separable kernel matrix K is that it can be expressed as the product of two vectors gRk1 and hR1k, which can also be regarded as two 1D filter kernels. In other words, K=gh. The resulting image we get by first applying g and then applying h to the image I is Igh. Show that IK=Igh