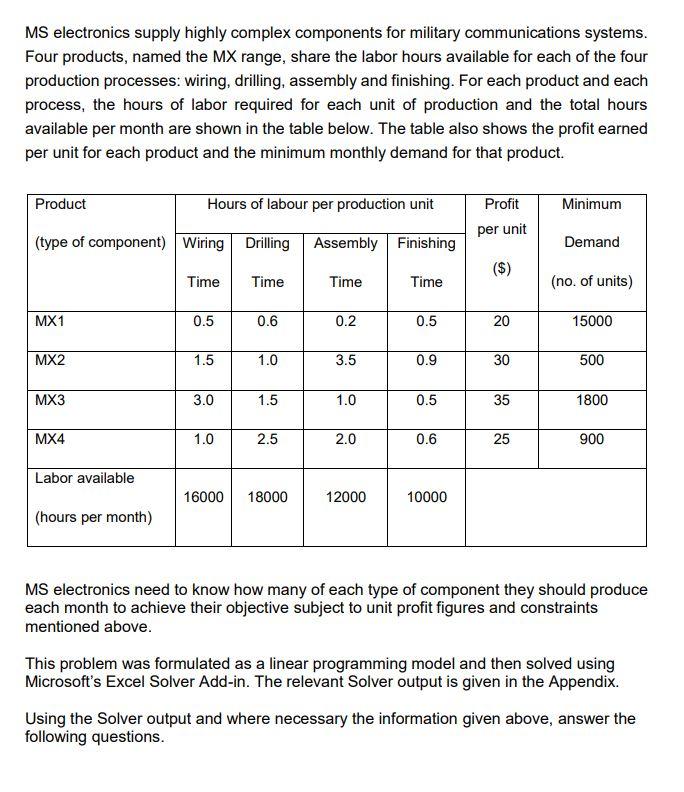
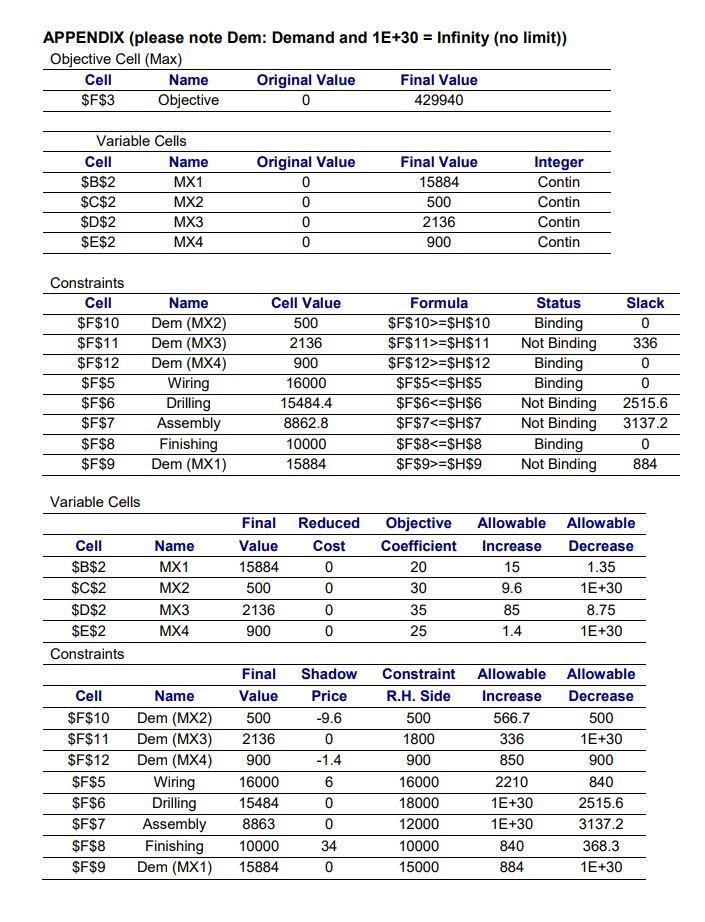
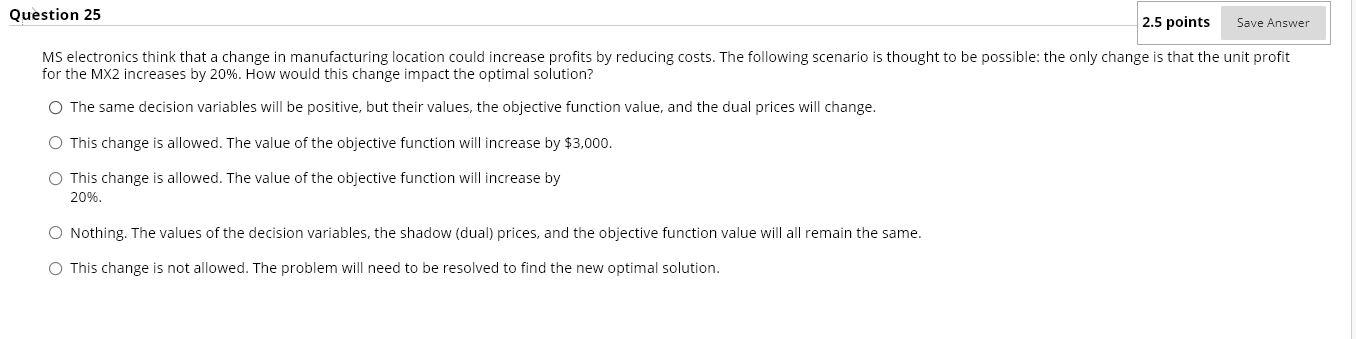
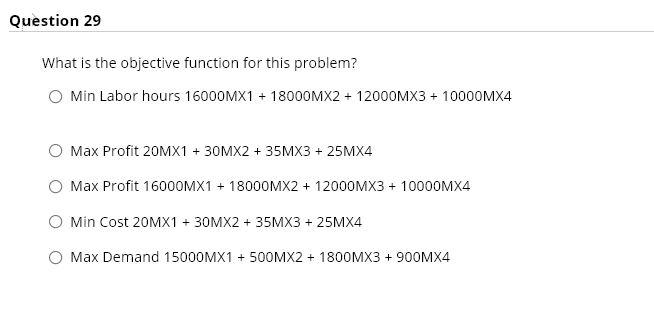
MS electronics supply highly complex components for military communications systems. Four products, named the MX range, share the labor hours available for each of the four production processes: wiring, drilling, assembly and finishing. For each product and each process, the hours of labor required for each unit of production and the total hours available per month are shown in the table below. The table also shows the profit earned per unit for each product and the minimum monthly demand for that product. Product Hours of labour per production unit Minimum Profit per unit (type of component) Wiring Drilling Assembly Finishing Demand ($) Time Time Time Time (no. of units) MX1 0.5 0.6 0.2 0.5 20 15000 MX2 1.5 1.0 3.5 0.9 30 500 MX3 3.0 1.5 1.0 0.5 35 1800 MX4 1.0 2.5 2.0 0.6 25 900 Labor available 16000 18000 12000 10000 (hours per month) MS electronics need to know how many of each type of component they should produce each month to achieve their objective subject to unit profit figures and constraints mentioned above. This problem was formulated as a linear programming model and then solved using Microsoft's Excel Solver Add-in. The relevant Solver output is given in the Appendix. Using the Solver output and where necessary the information given above, answer the following questions. APPENDIX (please note Dem: Demand and 1E+30 = Infinity (no limit)) Objective Cell (Max) Cell Name Original Value Final Value $F$3 Objective 0 429940 Variable Cells Cell Name $B$2 MX1 $C$2 MX2 $D$2 MX3 $E$2 MX4 Original Value 0 0 0 0 Final Value 15884 500 2136 900 Integer Contin Contin Contin Contin Constraints Cell $F$10 $F$11 $F$12 $F$5 $F$6 $F$7 $F$8 $F$9 Name Dem (MX2) Dem (MX3) Dem (MX4) Wiring Drilling Assembly Finishing Dem (MX1) Cell Value 500 2136 900 16000 15484.4 8862.8 10000 15884 Formula $F$10>=$H$10 $F$11>=$H$11 $F$12>=$H$12 $F$5=$H$9 Status Binding Not Binding Binding Binding Not Binding Not Binding Binding Not Binding Slack 0 336 0 0 2515.6 3137.2 0 884 Variable Cells Cell $B$2 $C$2 $D$2 $E$2 Constraints Name MX1 MX2 MX3 MX4 Final Value 15884 500 2136 900 Reduced Cost 0 0 Objective Coefficient 20 30 35 25 Allowable Allowable Increase Decrease 15 1.35 9.6 1E+30 85 8.75 1.4 1E+30 0 0 Cell $F$10 $F$11 $F$12 $F$5 $F$6 $F$7 $F$8 $F$9 Name Dem (MX2) Dem (MX3) Dem (MX4) Wiring Drilling Assembly Finishing Dem (MX1) Final Value 500 2136 900 16000 15484 8863 10000 15884 Shadow Price -9.6 0 -1.4 6 0 0 34 0 Constraint R.H. Side 500 1800 900 16000 18000 12000 10000 15000 Allowable Allowable Increase Decrease 566.7 500 336 1E+30 850 900 2210 840 1E+30 2515.6 1E+30 3137.2 840 368.3 884 1E+30 Question 21 From the output, which constraint(s) have surplus? ODEM (MX3) & DEM (MX1) Wiring & Drilling Drilling & Assembly DEM (MX2) & DEM (MX4) Assembly & Finishing Question 22 2.5 points A large number of staff will be leaving next month and, if no replacements can be found, 360 hours of finishing time will be lost. How would this affect the optimal solution? This change is allowed. The value of the objective function will increase by $12,240 ($34*360). This change is allowed. The value of the objective function will decrease by $12.240 ($34*360). O This change is allowed. The value of the objective function will decrease by $12,522.2 ($34*368.3). This change is allowed. The value of the objective function will increase by $12.522.2 ($34*368.3). This change is not allowed. The problem will need to be resolved to find the new optimal solution. Question 23 Which of the following is the wiring time constraint? 0.5MX1 + 1.5MX2 +3.0MX3 + 1.0MX4 > 16,000 20MX1 + 30MX2 + 35MX3 + 25MX4 S 16,000 0.5MX1 + 1.5MX2 + 3.0MX3 + 1.0MX4 = 16,000 O 15884MX1 + 500MX2 + 2136MX3 + 900MX4 S 16,000 O 0.5MX1 + 1.5MX2 + 3.0MX3 + 1.0MX4 $11,000, thus, MS should accept the offer. O Yes. Allowable increase is 2200 hours and worth $6*2200 = $13,200 > $11,000, thus, MS should accept the offer. O No. This change is not allowed. No. The problem will need to be resolved to answer this