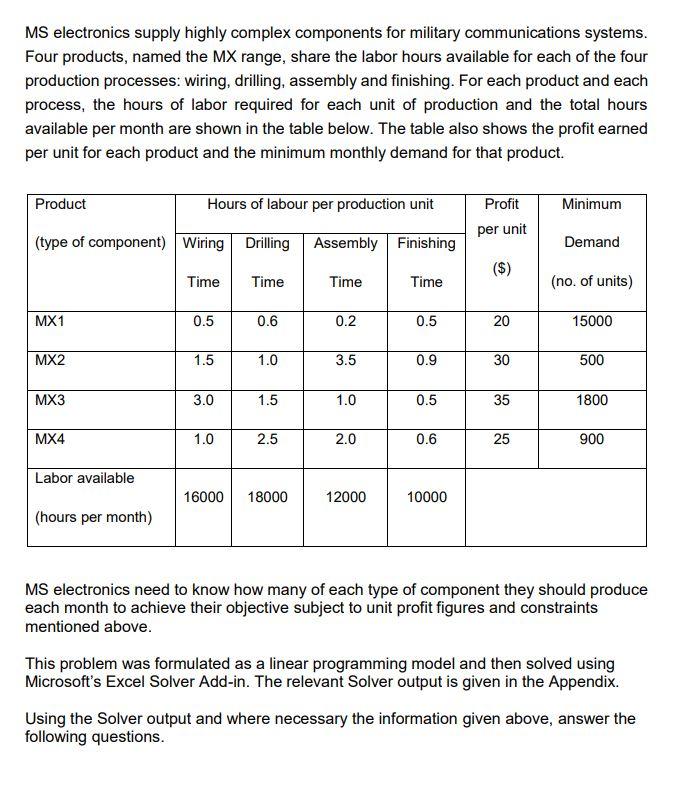
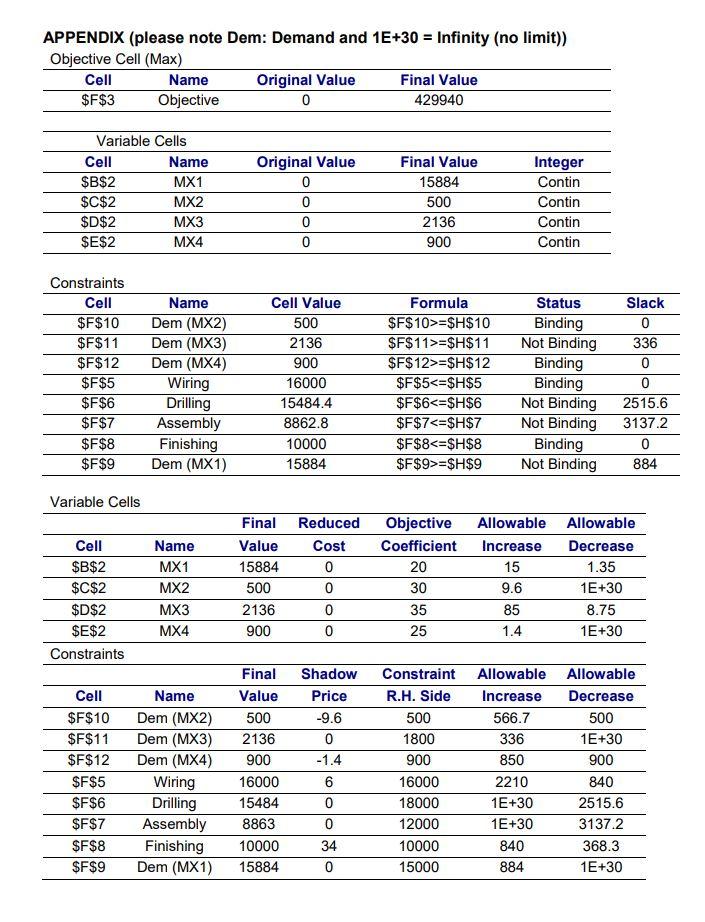
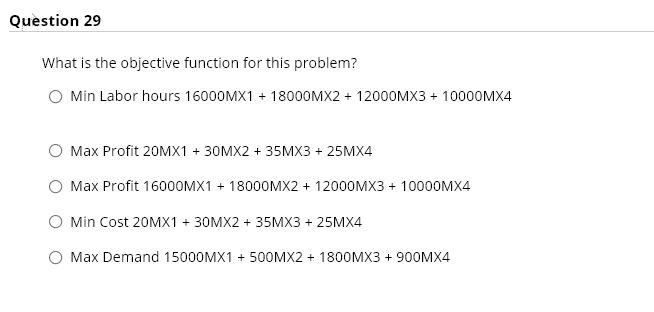
Question: MS electronics supply highly complex components for military communications systems. Four products, named the MX range, share the labor hours available for each of the



Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


