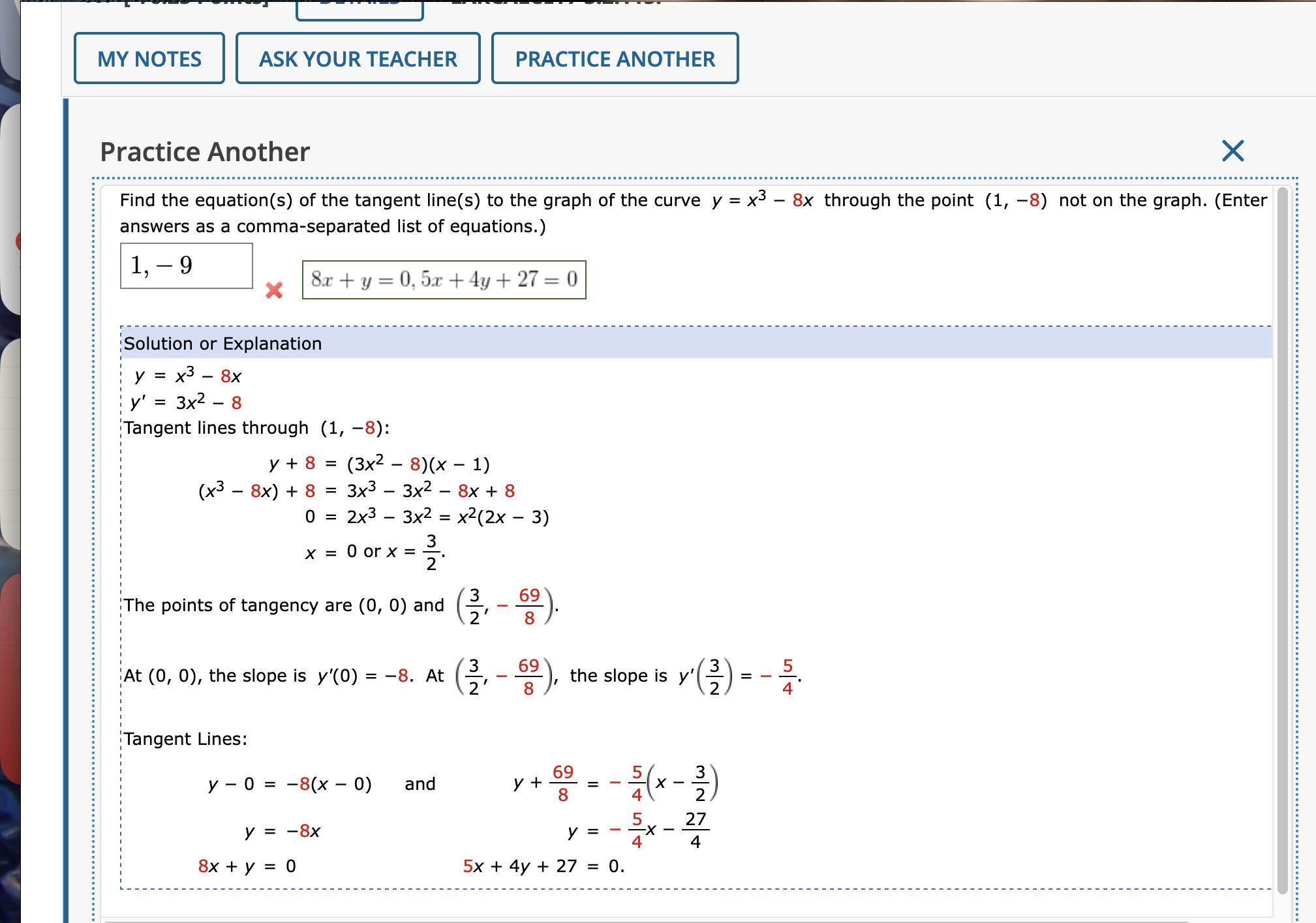
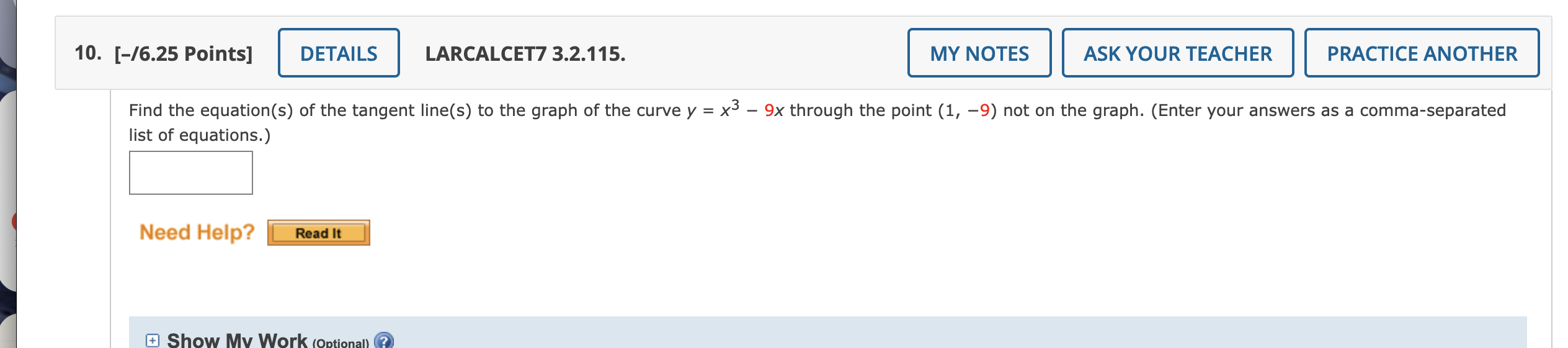
MY NOTES ASK YOUR TEACHER PRACTICE ANOTHER Practice Another X Find the equation(s) of the tangent line(s) to the graph of the curve y = x3 - 8x through the point (1, -8) not on the graph. (Enter answers as a comma-separated list of equations.) 1, - 9 X 8x + y = 0, 5x + 4y + 27 = 0 Solution or Explanation y = X3 - 8x y' = 3x2 - 8 Tangent lines through (1, -8): y + 8 = (3x2 - 8)(x - 1) (x3 - 8x) + 8 = 3x3 - 3x2 - 8x + 8 0 = 2x3 - 3x2 = x2(2x - 3) x = 0 or x = The points of tangency are (0, 0) and 8 At (0, 0), the slope is y'(0) = -8. At 69 8 ) ' the slope is y'S ) = - 7. Tangent Lines: y - 0 = -8(x - 0) and y + 69 5 X 8 4 y = -8X 27 y= -X - 4 4 8x+ y = 0 5x + 4y + 27 = 0.10. [-/6.25 Points] DETAILS LARCALCET7 3.2.115. MY NOTES ASK YOUR TEACHER PRACTICE ANOTHER Find the equation(s) of the tangent line(s) to the graph of the curve y = x3 - 9x through the point (1, -9) not on the graph. (Enter your answers as a comma-separated list of equations.) Need Help? Read It + Show My Work