my professor didn't use formula steps on problems but he only used answers...so please look at those all questions and solve those 2 with the formula steps

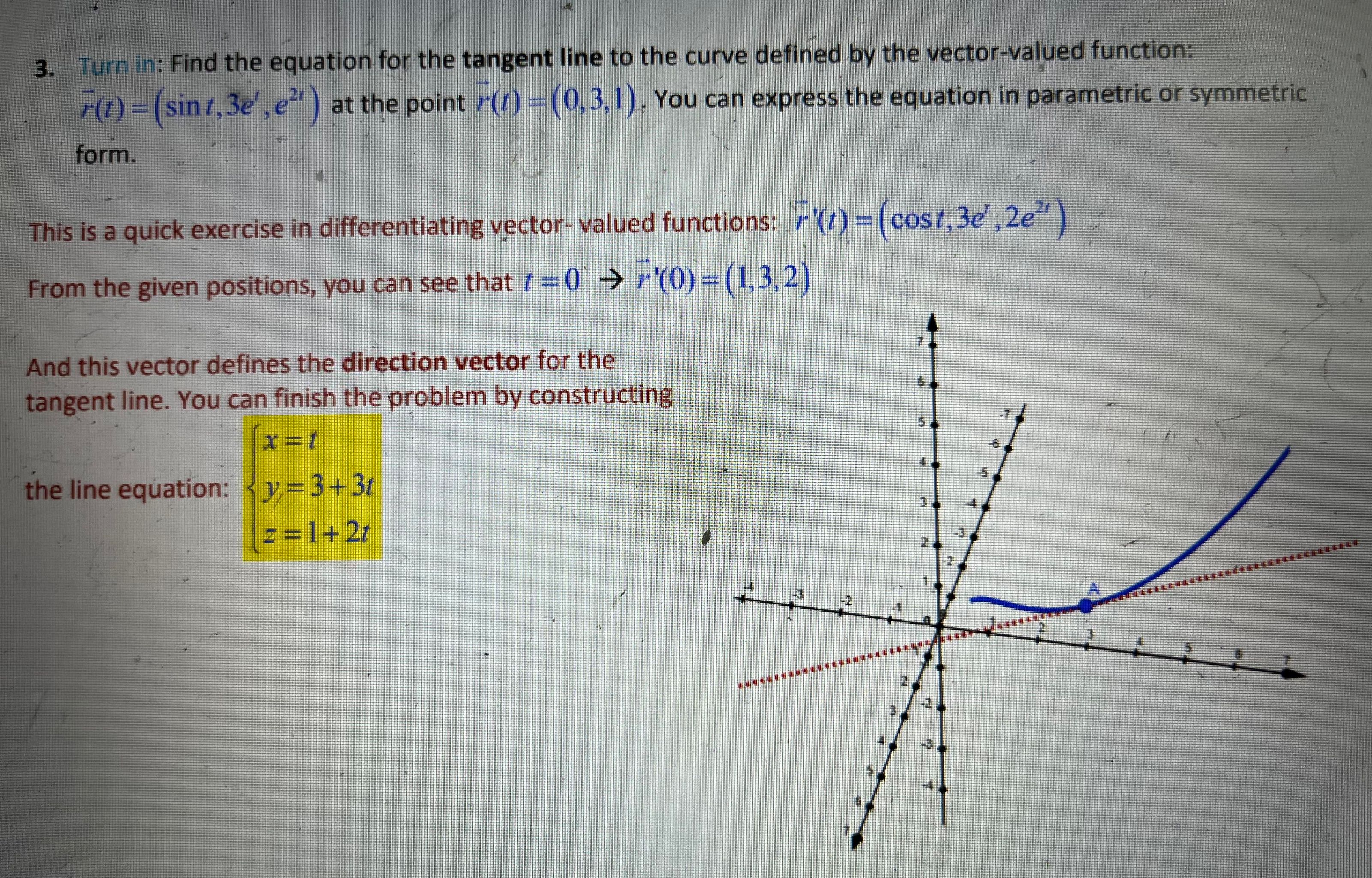
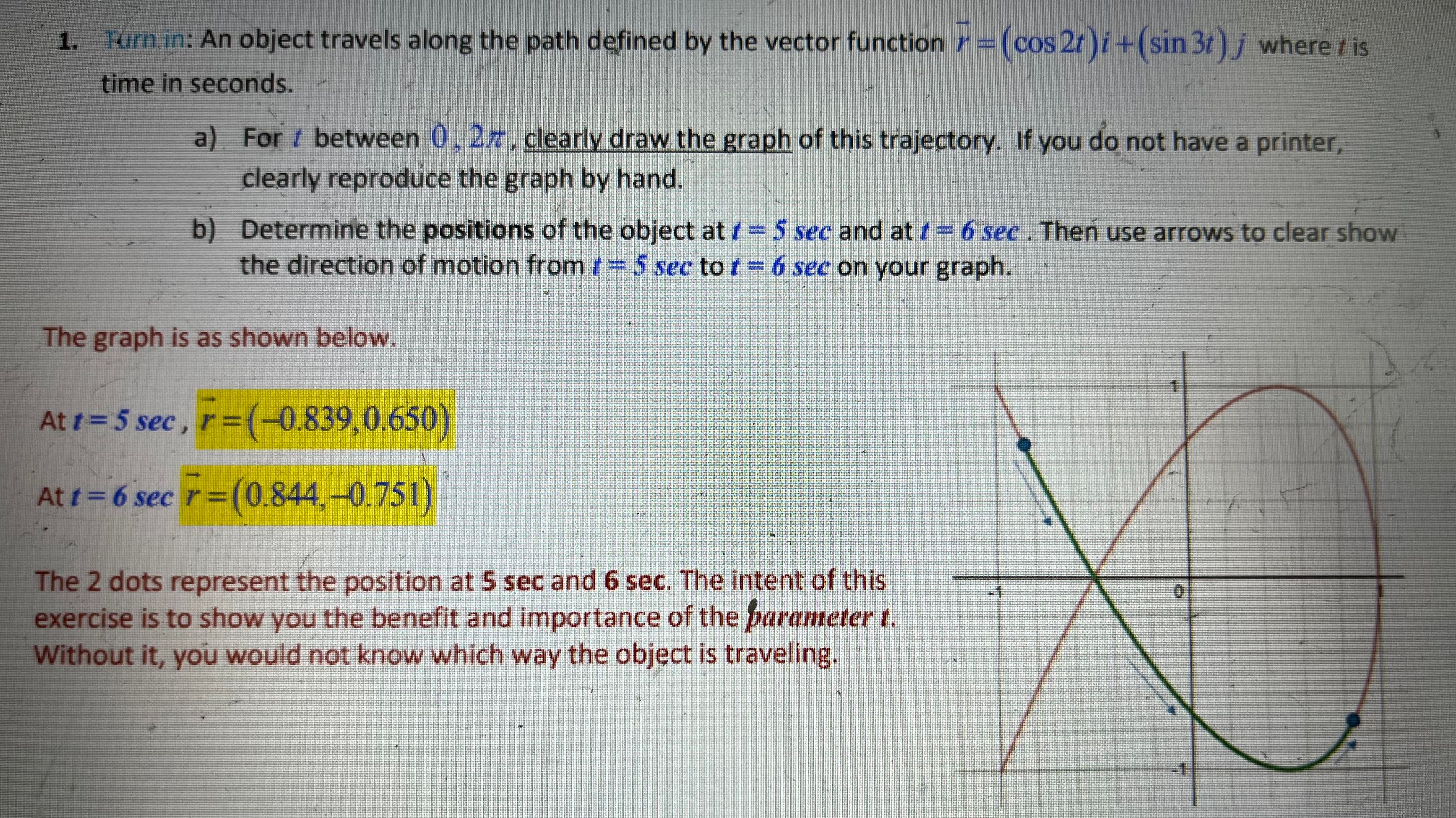
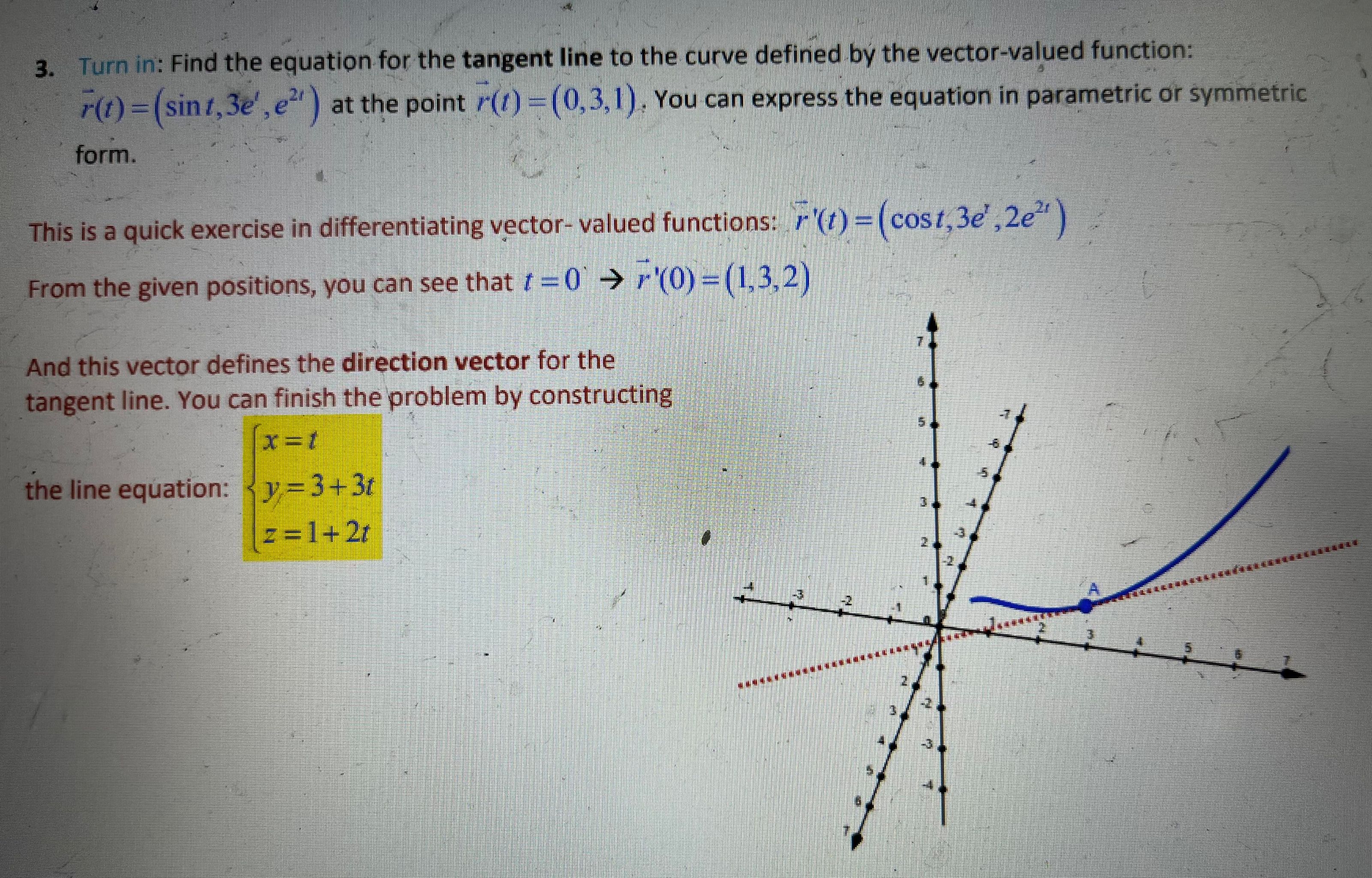
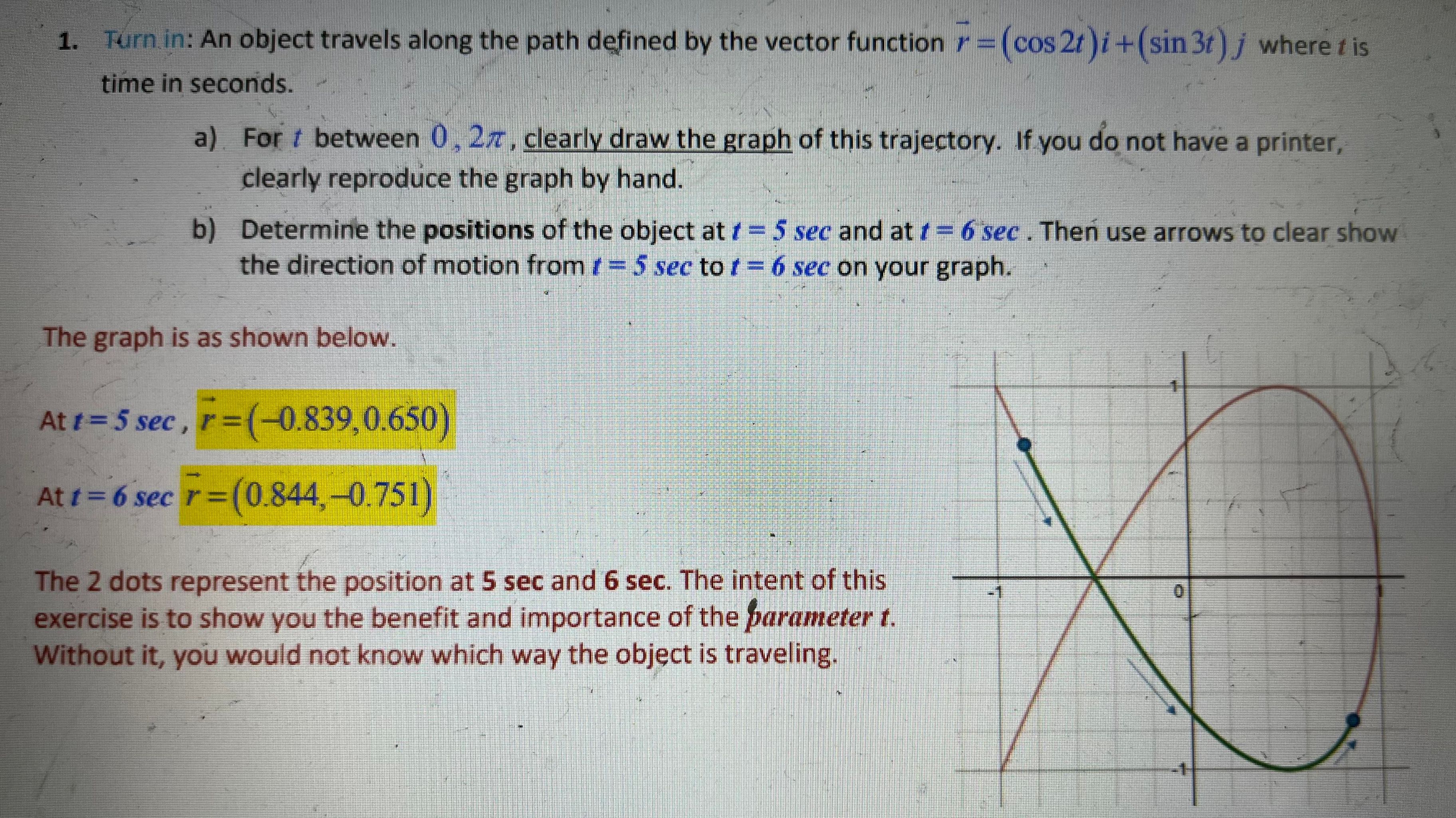
3. Turn in: Find the equation for the tangent line to the curve defined by the vector-valued function: r(1) = (sint, 3e', e" ) at the point r(/) =(0,3,1). You can express the equation in parametric or symmetric form. This is a quick exercise in differentiating vector- valued functions: r '(/) = (cost, 3e' ,2e" ) From the given positions, you can see that / = 0 > r'(0) = (1,3,2) And this vector defines the direction vector for the tangent line. You can finish the problem by constructing x =1 the line equation: Ry = 3+3t = =1+21. Turn in: An object travels along the path defined by the vector function r = (cos 2t )i + (sin 3t ) j where r is time in seconds. a) For / between 0, 2/r, clearly draw the graph of this trajectory. If you do not have a printer, clearly reproduce the graph by hand. b) Determine the positions of the object at ? = 5 sec and at f = 6 sec . Then use arrows to clear show the direction of motion from t = 5 sec to f = 6 sec on your graph. The graph is as shown below. At t =5 sec , r = (-0.839, 0.650) At t = 6 sec r = (0.844,-0.751) The 2 dots represent the position at 5 sec and 6 sec. The intent of this 0 exercise is to show you the benefit and importance of the parameter t. Without it, you would not know which way the object is traveling