need help with this physics lab

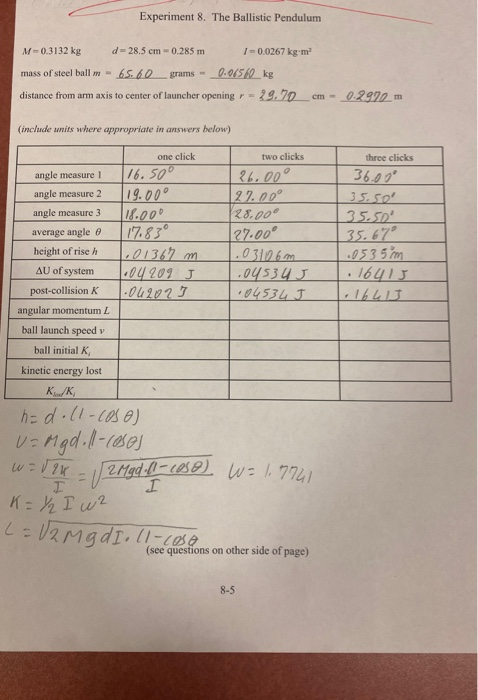
Purpose Experiment 8. The Ballistic Pendulum To examine a system applying ideas of conservation of both angular momentum and energy Apparatus Pasco ballistic pendulum, meter stick, pan balance Theory The ballistic pendulum consists of a spring-powered projectile launcher, a small steel ball, a ball catcher attached to a swinging arm, and an angular-measurement device to determine the angle through which the arm swings. In operation, the spring is initially compressed with the ball in front of the spring. When the spring is released from its initial position it gives the ball an initial velocity. Almost immediately after the ball exits the launcher it enters the catcher. The catching process is a completely inelastic collision. We have previously considered inelastic collisions for straight-line motion. In this case, though, the motion following the collision is a rotation about an axis. Thus, we apply the idea of conservation of angular momentum in our analysis of this system. Mechanical energy is lost during the collision but it is conserved in the motion following the collision. As the arm swings with the ball and ball-catcher moving upward kinetic energy is transformed into gravitational potential energy. At the point of maximum rotation the energy is entirely potential and is equal to the kinetic energy immediately after the collision. The next section provides the mathematical analysis for our system. The angular momentum of a 'point-like' object is given by: l=mvr. Equation (8-1) In Equation (8-1), m is the mass of the ball, v is its velocity as it leaves the launcher, and r is the distance between it (as it reaches the ball-catcher) and the axis of the arm. The angular momentum of an object with distributed mass in rotation about an axis is: L = 10. Equation (8-2) Here, I is the moment of inertia (also known as rotational inertia) of the ball-catcher with the ball and the arm to which it is attached, and co is its angular velocity. Immediately following the collision this value is the same as the angular momentum of the ball alone immediately prior to the collision. The kinetic energy of the rotating system is given by: 8-1