Needs to be modeled and solved in OPL/CPLEX

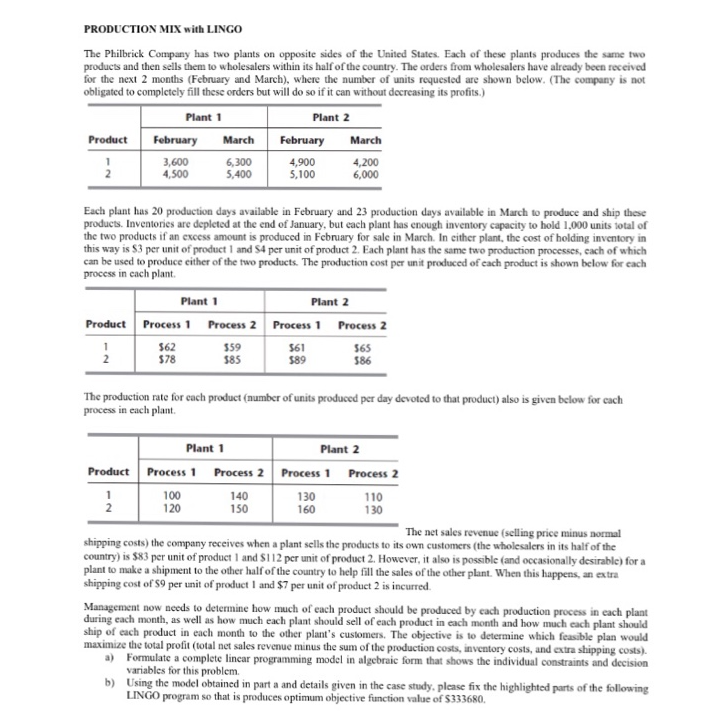
PRODUCTION MIX with LINGO The Philbrick Company has two plants on opposite sides of the United States. Each of these plants produces the same two products and then sells them to wholesalers within its half of the country. The orders from wholesalers have already been received for the next 2 months (February and March), where the number of units requested are shown below. (The company is not obligated to completely fill these orders but will do so if it can without decreasing its profits.) Plant 1 Plant 2 Product February March February March 3,600 6,300 4,900 4,200 4,500 5,400 5,100 6,000 Each plant has 20 production days available in February and 23 production days available in March to produce and ship these products. Inventories are depleted at the end of January, but each plant has enough inventory capacity to hold 1,000 units total of the two products if an excess amount is produced in February for sale in March. In either plant, the cost of holding inventory in this way is 63 per unit of product 1 and 4 per unit of product 2. Each plant has the same two production processes, cach of which can be used to produce either of the two products. The production cost per un it produced of each product is shown below for each process in each plant Plant 1 Plant 2 Product Process 1 Process 2 Process 1 Process 2 562 559 561 565 578 585 589 586 The production rate for each product (number of units produced per day devoted to that product) also is given below for cach process in each plant 100 Plant 1 Plant 2 Product Process 1 Process 2 Process 1 Process 2 1 140 130 110 120 150 160 130 The net sales revenue (selling price minus normal shipping costs) the company receives when a plant sells the products to its own customers (the wholesalers in its half of the country) is 883 per unit of product and $112 per unit of product 2. However, it also is possible (and occasionally desirable) for a plant to make a shipment to the other half of the country to help fill the sales of the other plant. When this happens, an extra shipping cost of S9 per unit of product and $7 per unit of product 2 is incurred. Management now needs to determine how much of each product should be produced by cach production process in cach plant during each month, as well as how much each plant should sell of each product in cach month and how much each plant should ship of each product in each month to the other plant's customers. The objective is to determine which feasible plan would maximize the total profit (total net sales revenue minus the sum of the production costs, inventory costs, and extra shipping costs). a) Formulate a complete lincar programming model in algebraic form that shows the individual constraints and decision variables for this problem b) Using the model obtained in part a and details given in the case study, please fix the highlighted parts of the following LINGO program so that is produces optimum objective function value of 5333680