Noise cancelation

We shall now use the LMS algorithm for canceling an additive noise from a signal. Denote by () a signal and () a noise. The input

signal is () = () + ().

We will want to build a filter that restores only () from () according to the following configuration The delay is chosen sufficiently large so that the signal noise () and ( ) are uncorrelated.

The output of the adaptive filter is the estimate

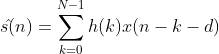
The error signal that is used in optimizing the filter coefficients is () = () ().

Due to the delay , the algorithm for adjusting the coefficients recursively becomes

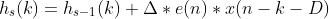
for 0 1, = 1,2 .

Write in Python a function lmsdelay, which implements this modified algorithm.

Test your function on the following input: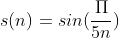

a Gaussian noise with zero mean and standard deviation equals to 0.2 (use the function np.random.normal), = 11, = 1000

Does the computed filter have a linear phase? Numerically draw the of its impulse response with resolution of 200 samples. Is it a low-pass filter, high-pass filter,? Compute the zeros of its -transform.