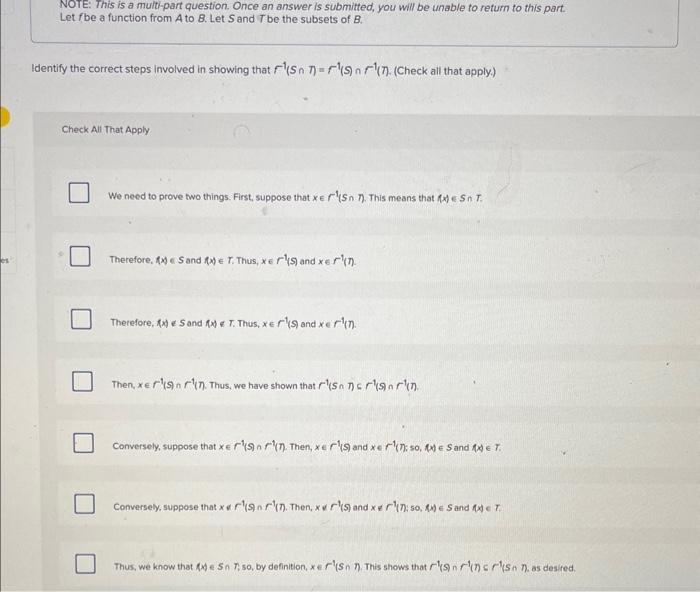
NOTE: This is a muith-part question. Once an answer is submitted, you will be unable to return to this part. Let f be a function from A to B. Let S and T be the subsets of B. Identify the correct steps involved in showing that f1(ST)=r1(S)f1(T). (Check all that apply.) Check All That Apply We need to prove two things. First, suppose that xF1(Sn). This means that f(x)ST. Therefore, f(x)S and f(x)T. Thus, xr1(S) and xf1(. Therefore, f(x)S and f(x)T. Thus, xf1(S) and xr1(n. Then, xf1(S)nr1(T). Thus, we have shown that r1(Snt)r1(S)r1(n. Conversely, suppose that xr1(S)f1(I). Then, xr1(S) and xr1(I) so, (x)S and f(x)T. Conversely, suppose that x/r1(S)nr1(D). Then, xr1(S) and xr1(D; so, Sx)S and fxT Thus, we know that {x)Snn so, by definition, xr1(Snn) This shows that r1(S)nr1(n)r1(Snn) as desited