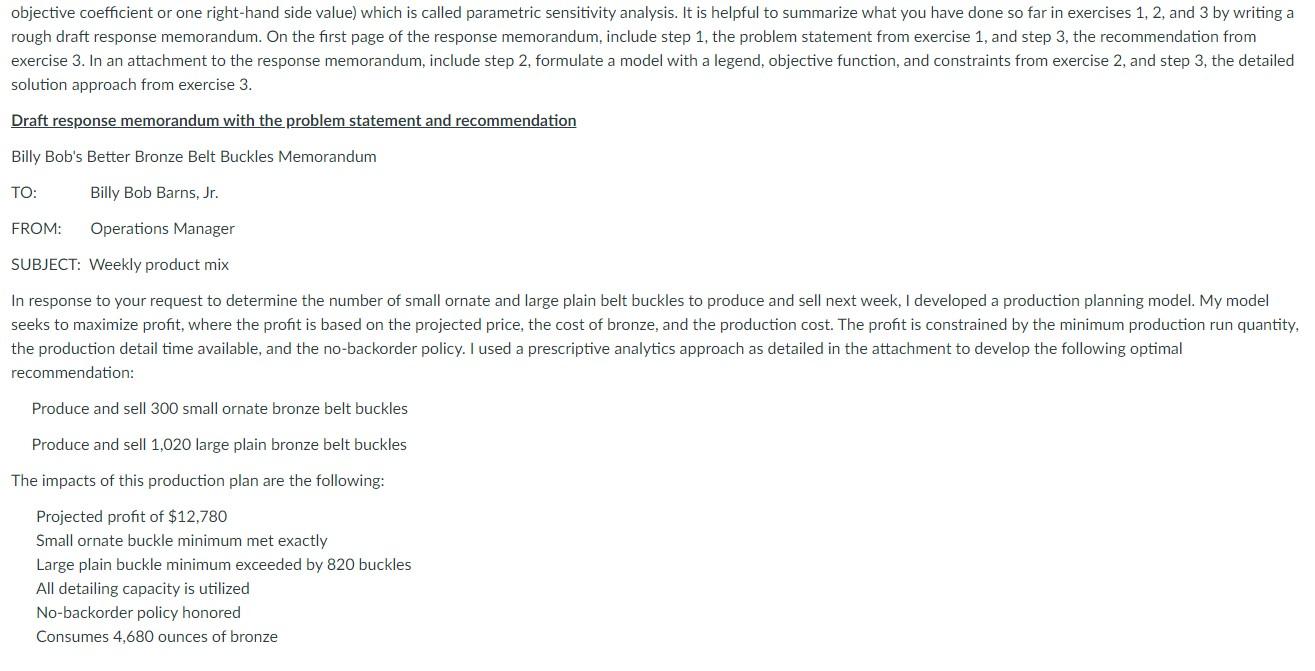
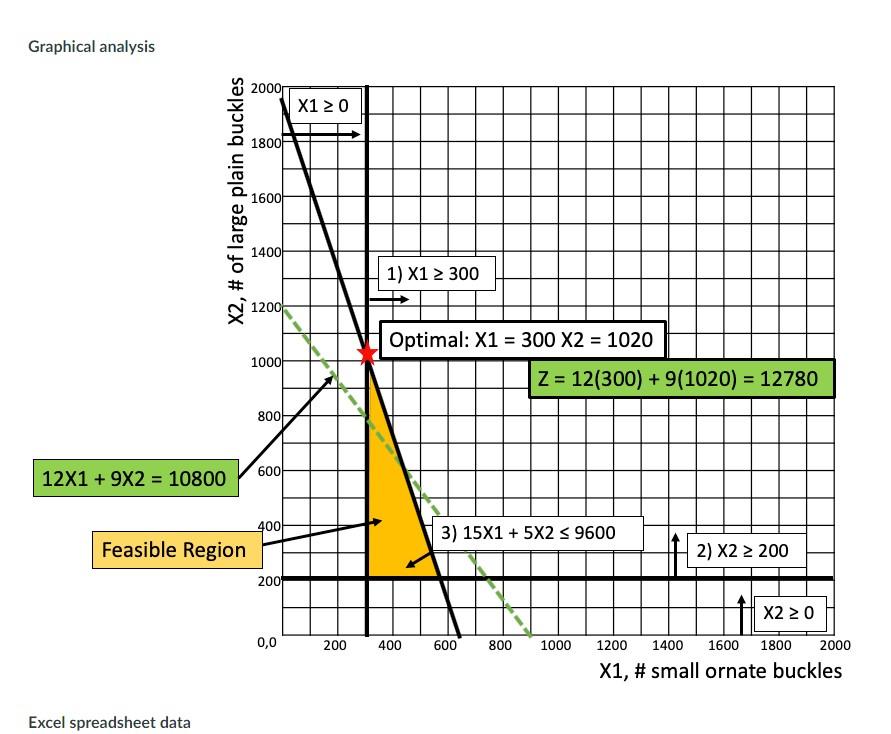
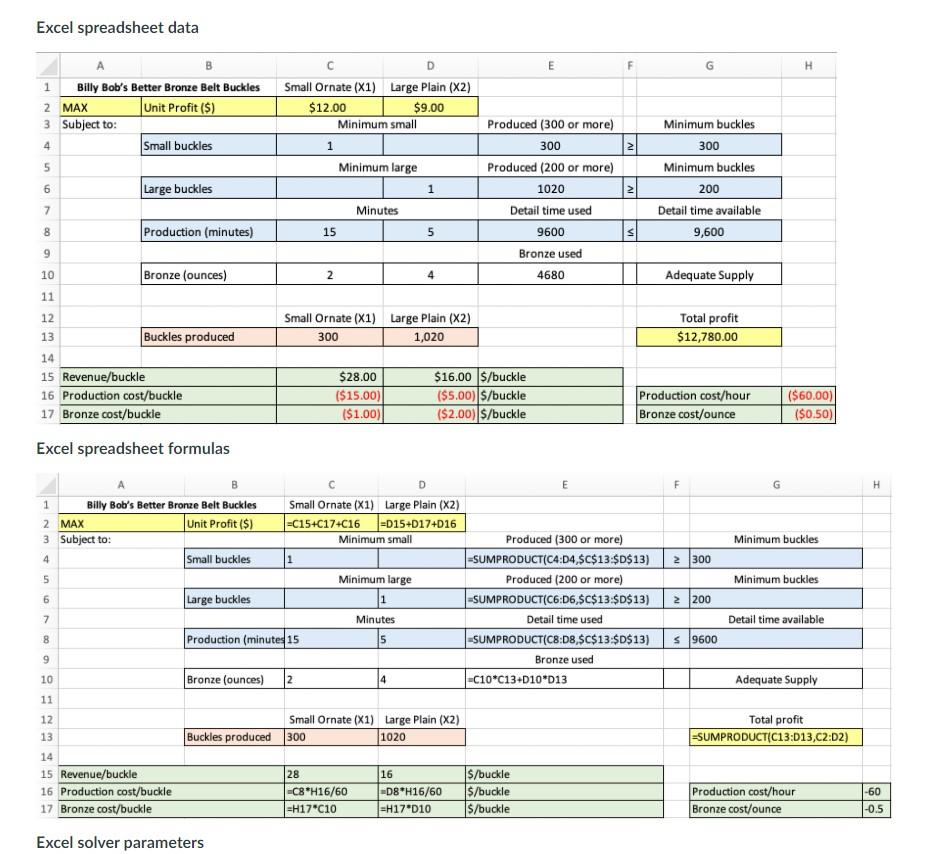
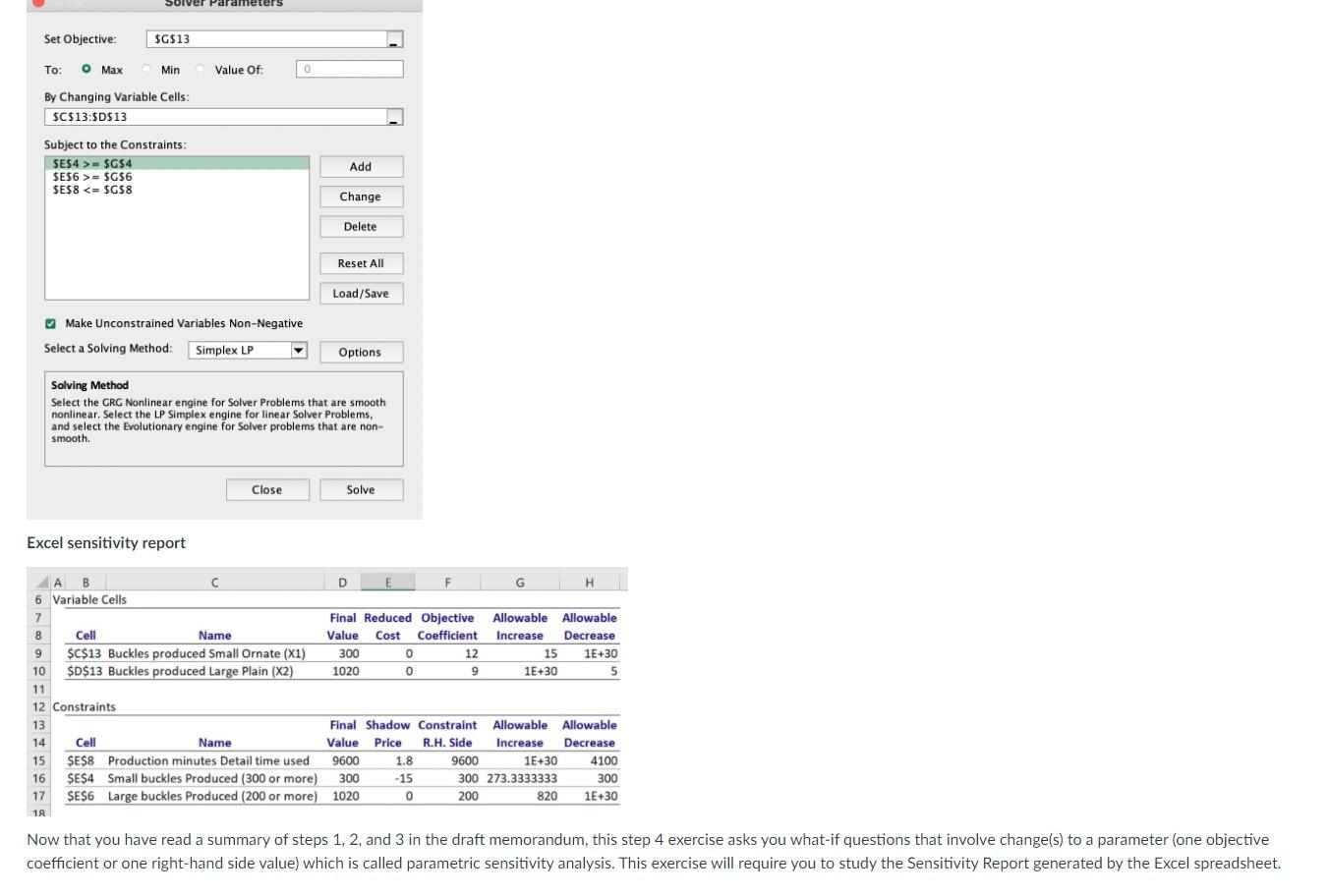
objective coefficient or one right-hand side value) which is called parametric sensitivity analysis. It is helpful to summarize what you have done so far in exercises 1, 2, and 3 by writing a rough draft response memorandum. On the first page of the response memorandum, include step 1, the problem statement from exercise 1, and step 3, the recommendation from exercise 3. In an attachment to the response memorandum, include step 2, formulate a model with a legend, objective function, and constraints from exercise 2, and step 3, the detailed solution approach from exercise 3. Draft response memorandum with the problem statement and recommendation Billy Bob's Better Bronze Belt Buckles Memorandum TO: Billy Bob Barns, Jr. FROM: Operations Manager SUBJECT: Weekly product mix In response to your request to determine the number of small ornate and large plain belt buckles to produce and sell next week, I developed a production planning model. My model seeks to maximize profit, where the profit is based on the projected price, the cost of bronze, and the production cost. The profit is constrained by the minimum production run quantity, the production detail time available, and the no-backorder policy. I used a prescriptive analytics approach as detailed in the attachment to develop the following optimal recommendation: Produce and sell 300 small ornate bronze belt buckles Produce and sell 1,020 large plain bronze belt buckles The impacts of this production plan are the following: Projected profit of $12.780 Small ornate buckle minimum met exactly Large plain buckle minimum exceeded by 820 buckles All detailing capacity is utilized No-backorder policy honored Consumes 4,680 ounces of bronze * Rough draft note 1: After performing sensitivity analysis, add details about the insights. Draft attachment to the response memorandum with the model and solution approach The prescriptive analytics solution approach used to develop the recommended production plan is based on the linear programming model and the graphical analysis and Excel analysis that follow. Linear programming model formulation Legend X1 = number of small ornate belt buckles to produce and sell X2 = number of large plain belt buckles to produce and sell Objective MAX 12X1 + 9X2 Max profit ($) Constraints 1X1 300 Production quantity minimum (small ornate buckles) 1X22 200 Production quantity minimum (large plain buckles) 15X1 + 5X2 = 9,600 Production detail time available (hours) X1 X2Z 0 Non-negativity/No-backorder policy (buckles) Graphical analysis Graphical analysis 2000 X1 20 1800 X2, # of large plain buckles 1600) 1400 1) X1 2 300 1200 Optimal: X1 = 300 X2 = 1020 1000 Z = 12(300) + 9(1020) = 12780 800 600 12X1 + 9X2 = 10800 400 Feasible Region 3) 15X1 + 5X2 S 9600 2) X2 > 200 2001 0,0 200 400 600 800 1000 1200 X220 1400 1600 1800 2000 X1, # small ornate buckles Excel spreadsheet data Excel spreadsheet data E H 1 Billy Bob's Better Bronze Belt Buckles 2 MAX Unit Profit ($) 3 Subject to: Small buckles D Small Ornate (X1) Large Plain (X2) $12.00 $9.00 Minimum small 1 Minimum large 4 2 5 Produced (300 or more) 300 Produced (200 or more) 1020 Detail time used 9600 Minimum buckles 300 Minimum buckles 200 Detail time available 9,600 6 Large buckles 1 IV 7 Minutes 8 Production (minutes) 15 5 9 Bronze used 10 Bronze (ounces) 2 4 4680 Adequate Supply 11 Small Ornate (X1) Large Plain (X2) 300 1,020 Total profit $12,780.00 12 13 Buckles produced 14 15 Revenue/buckle 16 Production cost/buckle 17 Bronze cost/buckle $28.00 ($15.00) ($1.00) $16.00 $/buckle ($5.00)|$/buckle ($2.00)|$/buckle Production cost/hour Bronze cost/ounce ($60.00) ($0.50) Excel spreadsheet formulas G H Minimum buckles 2 5 E F 1 Billy Bob's Better Bronze Belt Buckles Small Ornate (X1) Large Plain (X2) 2 MAX Unit Profit ($) =C15+C174016 |=D15+017+D16 3 Subject to: Minimum small Produced (300 or more) 4 Small buckles 1 -SUMPRODUCT(C4:04 $C$13:$D$13) 300 Minimum large Produced (200 or more) Large buckles -SUMPRODUCT(C6:06,$C$13:$D$13) 2 200 Minutes Detail time used Production (minutes 15 -SUMPRODUCT(C8:08,$C$13:$D$13) 9600 Bronze used Bronze (ounces) -C10*13-D10*D13 Minimum buckles 6 1 7 Detail time available 8 5 9 10 2 4 Adequate Supply 11 12 13 Small Ornate (X1) Large Plain (X2) Buckles produced 300 1020 Total profit =SUMPRODUCT(C13:013,02:02) 14 15 Revenue/buckle 16 Production cost/buckle 17 Bronze cost/buckle 28 -C8*H16/60 =H17C10 16 -D8*H16/60 =H17 *D10 $/buckle $/buckle $/buckle Production cost/hour Bronze cost/ounce -60 -0.5 Excel solver parameters solver parameters Set Objective: $G$13 : oMax Min Value Of 0 By Changing Variable Cells: $C$13:$D$13 Subject to the Constraints: SE$4 >= SG$4 SE56 >= $G$6 SE58 200 2001 0,0 200 400 600 800 1000 1200 X220 1400 1600 1800 2000 X1, # small ornate buckles Excel spreadsheet data Excel spreadsheet data E H 1 Billy Bob's Better Bronze Belt Buckles 2 MAX Unit Profit ($) 3 Subject to: Small buckles D Small Ornate (X1) Large Plain (X2) $12.00 $9.00 Minimum small 1 Minimum large 4 2 5 Produced (300 or more) 300 Produced (200 or more) 1020 Detail time used 9600 Minimum buckles 300 Minimum buckles 200 Detail time available 9,600 6 Large buckles 1 IV 7 Minutes 8 Production (minutes) 15 5 9 Bronze used 10 Bronze (ounces) 2 4 4680 Adequate Supply 11 Small Ornate (X1) Large Plain (X2) 300 1,020 Total profit $12,780.00 12 13 Buckles produced 14 15 Revenue/buckle 16 Production cost/buckle 17 Bronze cost/buckle $28.00 ($15.00) ($1.00) $16.00 $/buckle ($5.00)|$/buckle ($2.00)|$/buckle Production cost/hour Bronze cost/ounce ($60.00) ($0.50) Excel spreadsheet formulas G H Minimum buckles 2 5 E F 1 Billy Bob's Better Bronze Belt Buckles Small Ornate (X1) Large Plain (X2) 2 MAX Unit Profit ($) =C15+C174016 |=D15+017+D16 3 Subject to: Minimum small Produced (300 or more) 4 Small buckles 1 -SUMPRODUCT(C4:04 $C$13:$D$13) 300 Minimum large Produced (200 or more) Large buckles -SUMPRODUCT(C6:06,$C$13:$D$13) 2 200 Minutes Detail time used Production (minutes 15 -SUMPRODUCT(C8:08,$C$13:$D$13) 9600 Bronze used Bronze (ounces) -C10*13-D10*D13 Minimum buckles 6 1 7 Detail time available 8 5 9 10 2 4 Adequate Supply 11 12 13 Small Ornate (X1) Large Plain (X2) Buckles produced 300 1020 Total profit =SUMPRODUCT(C13:013,02:02) 14 15 Revenue/buckle 16 Production cost/buckle 17 Bronze cost/buckle 28 -C8*H16/60 =H17C10 16 -D8*H16/60 =H17 *D10 $/buckle $/buckle $/buckle Production cost/hour Bronze cost/ounce -60 -0.5 Excel solver parameters solver parameters Set Objective: $G$13 : oMax Min Value Of 0 By Changing Variable Cells: $C$13:$D$13 Subject to the Constraints: SE$4 >= SG$4 SE56 >= $G$6 SE58