Old MathJax webview

please help me with the bottom left that is all I have left on the sheet. H through K. Just need the correct formulas

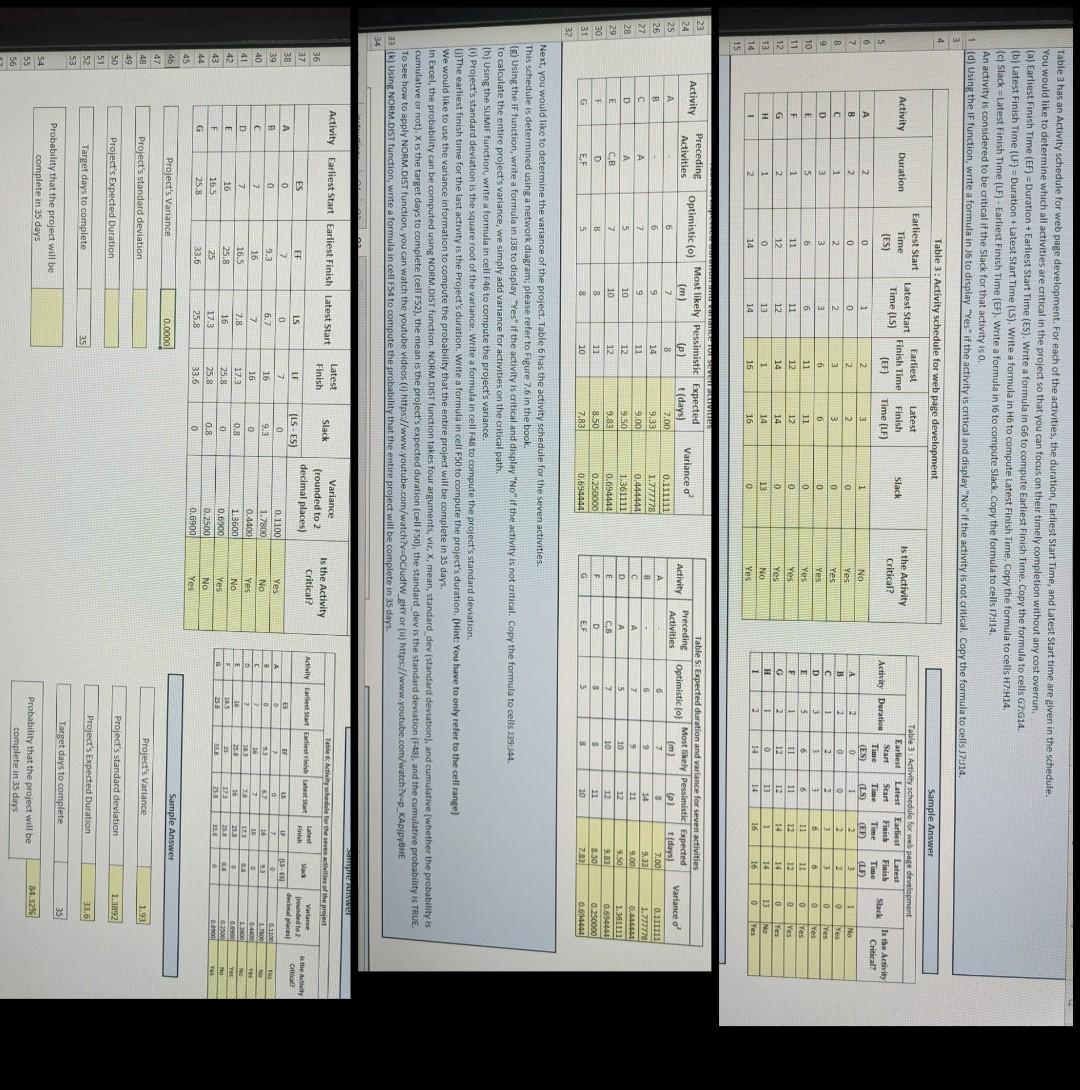
Table a has an Activity schedule for web page development. For each of the activities, the duration, Earliest Start Time, and Latest Start time are given in the schedule. You would like to determine which all activities are critical in the project so that you can focus their timely completion without any cost overrun (a) Earliest Finish Time (EF) = Duration + Earliest Start Time (ES). Write a formula in G6 to compute Earliest Finish Time. Copy the formula to cells 67:614. (b) Latest Finish Time (LF) = Duration +Latest Start Time (LS), Write a formula in H6 to compute Latest Finish Time. Copy the formula to cells H7:H14. (c) Slack=Latest Finish Time (LF) - Earliest Finish Time (EF). Write a formula in 16 to compute Slack. Copy the formula to cells 17:114. An activity is considered to be critical if the Slack for that activity is 0. 1 (d) Using the IF function, write a formula in 16 to display "Yes" if the activity is critical and display "No if the activity is not critical. Copy the formula to cells 17:14 Table 3: Activity schedule for web page development Sample Answer Activity Duration Earliest Start Time (ES) Earliest Latest Start Finish Time Time (LS) (EF) Latest Finish Time (LF) Slack Is the Activity Critical? 1 NO A B Yes 0 0 2 3 6 3 2 3 6 0 2 2 1 3 5 1 2 1 6 7 8 9. 10 11 12 18 14 15 Yes Yes 1 0 2 3 6 11 12 13 14 E F G H Table 3: Activity schedule for web page development Earliest Latest Earliest Latest Start Start Finish Activity Duration Finish Slack Is the Activity Tum Time T Critical SI ILS (E (LF A 2 0 2. 1 NO B 0 2 Yes 2 3 0 lyes D 1 6 6 0 Yes E 11 Yes 11 11 12 12 0 [res G 12 14 14 0 Yes 0 14 13 No 14 16 16 Yes 2 2 3 6 11 12 14 1 16 12 0 14 12 14 14 16 0 10 0 13 0 Yes Yes Yes NO Yes 1 2 Activity Preceding Activities Variance o Activity Variance o - 23 24 25 26 27 28 29 30 31 32 A B c D E F G SOLUTIONS Optimistic (0) Most likely Pessimistic Expected (m (p) t(days) 6 8 7.00 6 9 14 9.33 2 11 9.00 5 10 12 S SO 7 10 12 9.83 R 8 11 8.50 5 8 10 7.83 0.111111 1.777778 0.444444 1.361111 0.694444 0.250000 0.694444 A B c D E Table 5: Expected duration and variance for seven activities Preceding Optimistico) Most likely Pessimistic Expected Activities t(days) 6 7 3 7.00 6 9 14 9.33 A 9 9.00 5 10 12 9.50 CB z 10 12 3.33 D 11 3.50 FE 5 20 7.83 A CB D FE 0.111111 1.777778 0.48 1.351112 0.894444 0.250000 0.694044 G Next, you would like to determine the variance of the project. Table 6 has the activity schedule for the seven activities. This schedule is determined using a network diagram: please refer to Figure 7.6 in the book. () Using the IF function, write a formula in 38 to display "Yes" if the activity is critical and display "No" if the activity is not critical. Copy the formula to cells 139:44 To calculate the entire project's variance, we simply add variance for activities on the critical path. th) Using the SUMIF function, write a formula in cell F45 to compute the project's variance. (1) Project's standard deviation is the square foot of the variance. Write a formula in cell 48 to compute the project's standard deviation The earliest finish time for the last activity is the Project's duration. Write a formula in cell F50 to compute the project's duration (Hint: You have to only refer to the cell range) We would like to use the variance information to compute the probability that the entire project will be complete in 35 days. In Excel, the probability can be computed using NORM.DIST function. NORM.DIST function takes four arguments, vit, X, mean, standard dev (standard deviation), and cumulative (whether the probability is cumulative or not). X is the target days to complete (cell F52), the mean is the project's expected duration (cello), the standard dev is the standard deviation (F48), and the cumulative probability is TRUE To see how to apply NORM.DIST function, you can watch the youtube videos (0) https://www.youtube.com/watch?v.OC) udfw_ghY or (0) https://www.youtube.com/watch?v=p_KAPPYBHE 23(k) Using NORM.DIST function write a formula in cell F54 to compute the probability that the entire project will be complete in 35 days. 34 MET Activity Earliest Start Earliest Finish Latest Start Latest Finish Slack Variance (rounded to decimal places) Is the Activity Critical? Table Activity schedule for the site of the project Earliest start that start Latest Variante frowded to Activity 36 37 38 39 FF IS ES 0 Is the Activity G decimal 5 U A B LA LS- 3 1 Tos No Tes 7 (LS-ES) 0 93 0 0.8 0 0.8 Yes No Yes No 10 9.3 16 165 25.8 25 32.6 LI 7 16 16 17.3 25.8 25,8 33 0 6.7 2 78 16 173 25.8 41 42 43 44 7 7 16 16.5 25.8 16 TE 23 0.1100 1.7800 0.4400 1.3600 0.6900 0.2500 0.6900 D E F G 15 16 17800 0400 1.15 0.6 0.3500 F Yes Yer No Yes LE 0 No Yes 45 Project's Variance 0.0000 Sample Answer Project's standard deviation Project's Variance 1.93 45 47 48 49 50 51 52 53 Project's standard deviation Project's Expected Duration 1.3892 Target days to complete Project's Expected Duration 25 33.6 Target days to complete 35 54 Probability that the project will be complete in 35 days Probability that the project will be complete in 35 days Table a has an Activity schedule for web page development. For each of the activities, the duration, Earliest Start Time, and Latest Start time are given in the schedule. You would like to determine which all activities are critical in the project so that you can focus their timely completion without any cost overrun (a) Earliest Finish Time (EF) = Duration + Earliest Start Time (ES). Write a formula in G6 to compute Earliest Finish Time. Copy the formula to cells 67:614. (b) Latest Finish Time (LF) = Duration +Latest Start Time (LS), Write a formula in H6 to compute Latest Finish Time. Copy the formula to cells H7:H14. (c) Slack=Latest Finish Time (LF) - Earliest Finish Time (EF). Write a formula in 16 to compute Slack. Copy the formula to cells 17:114. An activity is considered to be critical if the Slack for that activity is 0. 1 (d) Using the IF function, write a formula in 16 to display "Yes" if the activity is critical and display "No if the activity is not critical. Copy the formula to cells 17:14 Table 3: Activity schedule for web page development Sample Answer Activity Duration Earliest Start Time (ES) Earliest Latest Start Finish Time Time (LS) (EF) Latest Finish Time (LF) Slack Is the Activity Critical? 1 NO A B Yes 0 0 2 3 6 3 2 3 6 0 2 2 1 3 5 1 2 1 6 7 8 9. 10 11 12 18 14 15 Yes Yes 1 0 2 3 6 11 12 13 14 E F G H Table 3: Activity schedule for web page development Earliest Latest Earliest Latest Start Start Finish Activity Duration Finish Slack Is the Activity Tum Time T Critical SI ILS (E (LF A 2 0 2. 1 NO B 0 2 Yes 2 3 0 lyes D 1 6 6 0 Yes E 11 Yes 11 11 12 12 0 [res G 12 14 14 0 Yes 0 14 13 No 14 16 16 Yes 2 2 3 6 11 12 14 1 16 12 0 14 12 14 14 16 0 10 0 13 0 Yes Yes Yes NO Yes 1 2 Activity Preceding Activities Variance o Activity Variance o - 23 24 25 26 27 28 29 30 31 32 A B c D E F G SOLUTIONS Optimistic (0) Most likely Pessimistic Expected (m (p) t(days) 6 8 7.00 6 9 14 9.33 2 11 9.00 5 10 12 S SO 7 10 12 9.83 R 8 11 8.50 5 8 10 7.83 0.111111 1.777778 0.444444 1.361111 0.694444 0.250000 0.694444 A B c D E Table 5: Expected duration and variance for seven activities Preceding Optimistico) Most likely Pessimistic Expected Activities t(days) 6 7 3 7.00 6 9 14 9.33 A 9 9.00 5 10 12 9.50 CB z 10 12 3.33 D 11 3.50 FE 5 20 7.83 A CB D FE 0.111111 1.777778 0.48 1.351112 0.894444 0.250000 0.694044 G Next, you would like to determine the variance of the project. Table 6 has the activity schedule for the seven activities. This schedule is determined using a network diagram: please refer to Figure 7.6 in the book. () Using the IF function, write a formula in 38 to display "Yes" if the activity is critical and display "No" if the activity is not critical. Copy the formula to cells 139:44 To calculate the entire project's variance, we simply add variance for activities on the critical path. th) Using the SUMIF function, write a formula in cell F45 to compute the project's variance. (1) Project's standard deviation is the square foot of the variance. Write a formula in cell 48 to compute the project's standard deviation The earliest finish time for the last activity is the Project's duration. Write a formula in cell F50 to compute the project's duration (Hint: You have to only refer to the cell range) We would like to use the variance information to compute the probability that the entire project will be complete in 35 days. In Excel, the probability can be computed using NORM.DIST function. NORM.DIST function takes four arguments, vit, X, mean, standard dev (standard deviation), and cumulative (whether the probability is cumulative or not). X is the target days to complete (cell F52), the mean is the project's expected duration (cello), the standard dev is the standard deviation (F48), and the cumulative probability is TRUE To see how to apply NORM.DIST function, you can watch the youtube videos (0) https://www.youtube.com/watch?v.OC) udfw_ghY or (0) https://www.youtube.com/watch?v=p_KAPPYBHE 23(k) Using NORM.DIST function write a formula in cell F54 to compute the probability that the entire project will be complete in 35 days. 34 MET Activity Earliest Start Earliest Finish Latest Start Latest Finish Slack Variance (rounded to decimal places) Is the Activity Critical? Table Activity schedule for the site of the project Earliest start that start Latest Variante frowded to Activity 36 37 38 39 FF IS ES 0 Is the Activity G decimal 5 U A B LA LS- 3 1 Tos No Tes 7 (LS-ES) 0 93 0 0.8 0 0.8 Yes No Yes No 10 9.3 16 165 25.8 25 32.6 LI 7 16 16 17.3 25.8 25,8 33 0 6.7 2 78 16 173 25.8 41 42 43 44 7 7 16 16.5 25.8 16 TE 23 0.1100 1.7800 0.4400 1.3600 0.6900 0.2500 0.6900 D E F G 15 16 17800 0400 1.15 0.6 0.3500 F Yes Yer No Yes LE 0 No Yes 45 Project's Variance 0.0000 Sample Answer Project's standard deviation Project's Variance 1.93 45 47 48 49 50 51 52 53 Project's standard deviation Project's Expected Duration 1.3892 Target days to complete Project's Expected Duration 25 33.6 Target days to complete 35 54 Probability that the project will be complete in 35 days Probability that the project will be complete in 35 days