Only part 2 (Loop Invariant) needs to be solved.

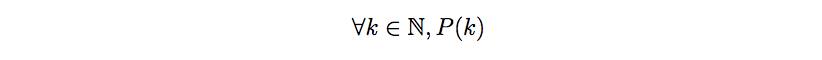
Problem 2. (10 MARKs) Iterative Program Correctness. One of your tasks in this assign ment is to write a proof that a program works correctly, that is, you need to prove that for all possible inputs, assuming the precondition is satisfied, the postcondition is satisfied after a finite number of steps This exercise aims to prove the correctness of the following program: def mult (m,n) : # Pre-condition: m,n are natural numbers """ Multiply natural numbers m and n """ 1 2 # Main loop while not x 0: 4 7. 8 elif x % 3-2 : 10. x-x + 1 xx div 3 12. 13. 14 # post condition : z = mn return z Let k denote the iteration number (starting at 0) of the Main Loop starting at line 5 ending at line 12. We will denote Ik the iteration k of the Main Loop. Also for each iteration, let Tk, Vk, 2k denote the values of the variables x, y, z at line 5 (the staring line) of Ik 1. (5 Marks) Termination. Need to prove that for all natural numbers n, m, there exist an iteration k, such that rk-0 at the beginning of 1k, that is at line 5 HINT: You may find helpful to prove this helper statement first: For all natural numbers k, xk > Ck+1 2 0. (Hint: do not use induction). 2. (2 Marks) Loop invariant Let P(k) be the predicate: At the end of Ik (line 12), Using induction, prove the following statement mn-Xkyk. Problem 2. (10 MARKs) Iterative Program Correctness. One of your tasks in this assign ment is to write a proof that a program works correctly, that is, you need to prove that for all possible inputs, assuming the precondition is satisfied, the postcondition is satisfied after a finite number of steps This exercise aims to prove the correctness of the following program: def mult (m,n) : # Pre-condition: m,n are natural numbers """ Multiply natural numbers m and n """ 1 2 # Main loop while not x 0: 4 7. 8 elif x % 3-2 : 10. x-x + 1 xx div 3 12. 13. 14 # post condition : z = mn return z Let k denote the iteration number (starting at 0) of the Main Loop starting at line 5 ending at line 12. We will denote Ik the iteration k of the Main Loop. Also for each iteration, let Tk, Vk, 2k denote the values of the variables x, y, z at line 5 (the staring line) of Ik 1. (5 Marks) Termination. Need to prove that for all natural numbers n, m, there exist an iteration k, such that rk-0 at the beginning of 1k, that is at line 5 HINT: You may find helpful to prove this helper statement first: For all natural numbers k, xk > Ck+1 2 0. (Hint: do not use induction). 2. (2 Marks) Loop invariant Let P(k) be the predicate: At the end of Ik (line 12), Using induction, prove the following statement mn-Xkyk