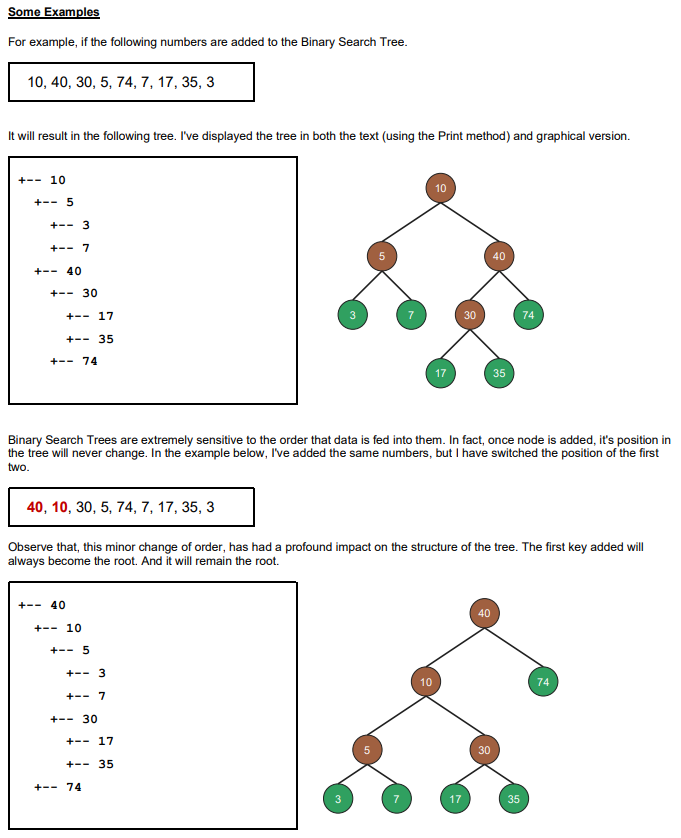
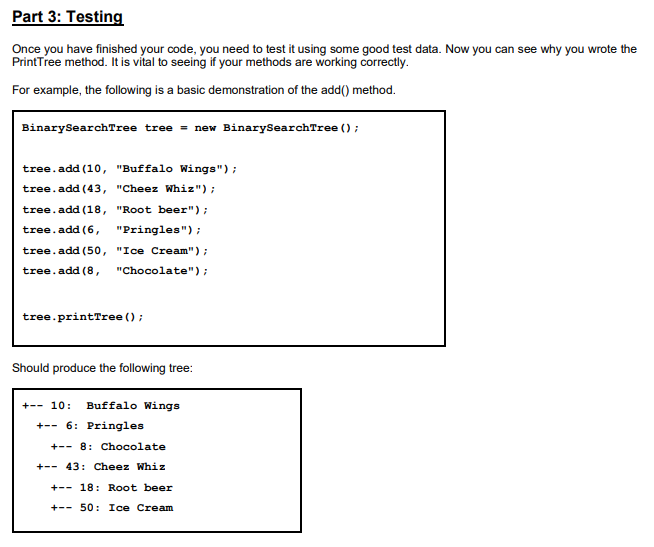
you are going to create a Binary Search Tree (BST) with a minimal interface. You don't have to balance the tree. In fact, don't even try it yet. We are creating a very basic tree class. For the sake of testing, we are going to restrict this tree to use Integers rather than the generic Object class. Like all programming assignments, work on it in parts. Part 1: Node Class Overview In recursively defined structures, like trees, all the coding (and complexity) is found in the recursive structure itself. In the case of trees, the node will contain the vast amount of the logic and behavior. The node will use a Key-Value system. The key is used to store and find nodes. The value field is completely passive.. Interface Create a very basic node class. All this requires is a left and right link (to another node) and a generic data field. It should also have a few constructors. In particular, you need one that will create a node with links to two other nodes. public class Node Node Node int void Node (int key, string value) void left right string value key print (int indent) add (int key, String value) Constructor that assigns the value and key. The key. This key will be used to store the node into the tree. The value that the node contains. This method will the structure of the tree. One node will be printed per line. You should use preorder tree traversal. Feel free to redirect the stream if you like. Please see the pseudocode below. Adds the key to the correct position in the BST. If the key already exists, do nothing. Pseudocode Class Node Node left Node right int key string value All your methods go here End Class Adding a Key To add a key, you will write a recursive method that will either recurse to the left or right - depending on the key. Whenever it can no longer recurse left or right, a new node is simply added. Method add (int newKey, string newValue) If this node's key < newKey then If left isn't null else End If left.add(newkey, newValue) End If else create a new left child for this node. If this node's key > newKey then If right isn't null End If End Method right.add(newkey, newValue) create a right left child for this node. End If Printing the Tree To print the tree, you will use recursion using a preorder depth-first traversal. Don't worry, it is not hard. Function Print (int indent) Print spaces for indent Print the "+" Print this.value and a newline left.print(indent + 1) right.print (indent + 1) End Function Part 2: BinarySearchTree Class Overview The main class will contain virtually node code. Instead, this class is used to start recursion on the root node. All key/values are added to the using the add() method. It will find the correct position in the tree and store it there. Interface Just like before, the BinarySearch Tree's methods will start recursion on the Node class. public class BinarySearchTree string void void string Pseudocode BinarySearchTree () about () end class print() add (int key, string value) find (int key) class BinarySearchTree private Node root All your methods go here Constructor. Returns text about you - the author of this class. Start recursion from the root node. Note: It starts with an indent of 0. Adds the key to the correct position in the BST. If the key already exists, do nothing. So, basically, you are creating a proper-set of numbers. Finds a node with the key and returns its value. If the node is not found, you can return an empty string. Some Examples For example, if the following numbers are added to the Binary Search Tree. 10, 40, 30, 5, 74, 7, 17, 35, 3 It will result in the following tree. I've displayed the tree in both the text (using the Print method) and graphical version. +10 +-- 5 +3 + 7 +40 +30 +17 +35 +-- 74 40, 10, 30, 5, 74, 7, 17, 35, 3 +40 +10 + 5 + + +30 3 7 Binary Search Trees are extremely sensitive to the order that data is fed into them. In fact, once node is added, it's position in the tree will never change. In the example below, I've added the same numbers, but I have switched the position of the first two. +17 +35 +-- 74 3 Observe that, this minor change of order, has had a profound impact on the structure of the tree. The first key added will always become the root. And it will remain the root. w 7 7 10 17 10 30 17 40 40 35 30 74 35 4 74 Part 3: Testing Once you have finished your code, you need to test it using some good test data. Now you can see why you wrote the PrintTree method. It is vital to seeing if your methods are working correctly. For example, the following is a basic demonstration of the add() method. Binary SearchTree tree = new BinarySearchTree (); tree.add (10, "Buffalo Wings"); tree.add(43, "Cheez Whiz"); tree.add(18, "Root beer"); tree.add (6, "Pringles"); tree.add(50, "Ice Cream"); tree.add (8, "Chocolate"); tree.printTree (); Should produce the following tree: +- 10: Buffalo Wings +6: Pringles +8: Chocolate +43: Cheez Whiz +18: Root beer + 50: Ice Cream