p is the average process time (days), m is the number of servers, and R_p is the total capacity rate of each station (unit/day). Assume that the final assembly (Station 4) requires one part from Path 1 and one part from Path 2 to complete one finished product.

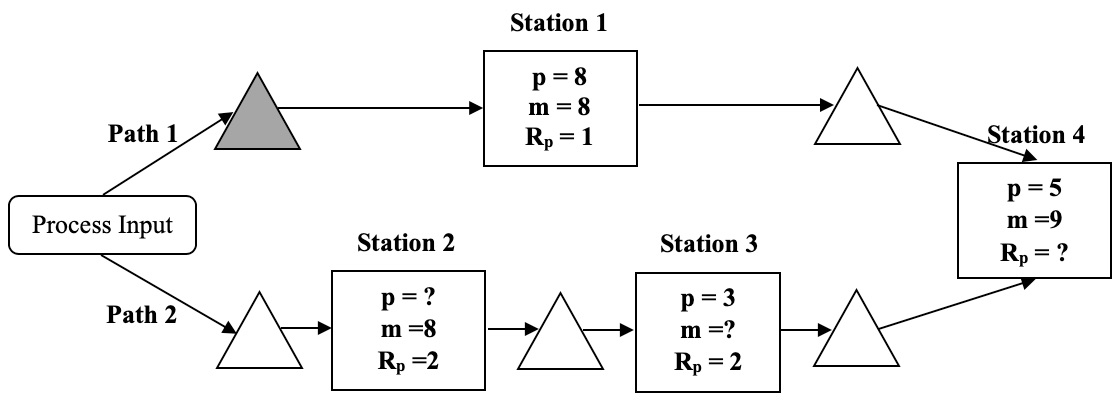
a. Fill out the unknowns in the process flow diagram

Station 2	p
Station 3	m
Station 4	Rp

b. What is the theoretical flow time of completing the entire process? Justify your answer.

c. What is the maximum possible rate of production that this system can achieve under the current configuration? Justify your answer.

d. If 0.9 parts are released into both paths every day for processing, what is the (actual) utilization of each station?

e. Suppose that jobs are released to Station 1 at the rate of 0.9 parts per day, and the inter-arrival time distribution has a coefficient of variation CV_a = 1. The coefficient of variation for Station 1s processing time equals CV_p = 1. Compute the average delay that a job would experience at Station 1 and the average number of units in the highlighted buffer (the one before Station 1).

Station 1 p = 8 m = 8 Path 1 Rp = 1 Station 4 Process Input p = 5 m =9 Rp = ? Station 2 Station 3 Path 2 p = 3 p = ? m=8 Rp =2 m=? Rp = = 2 ^