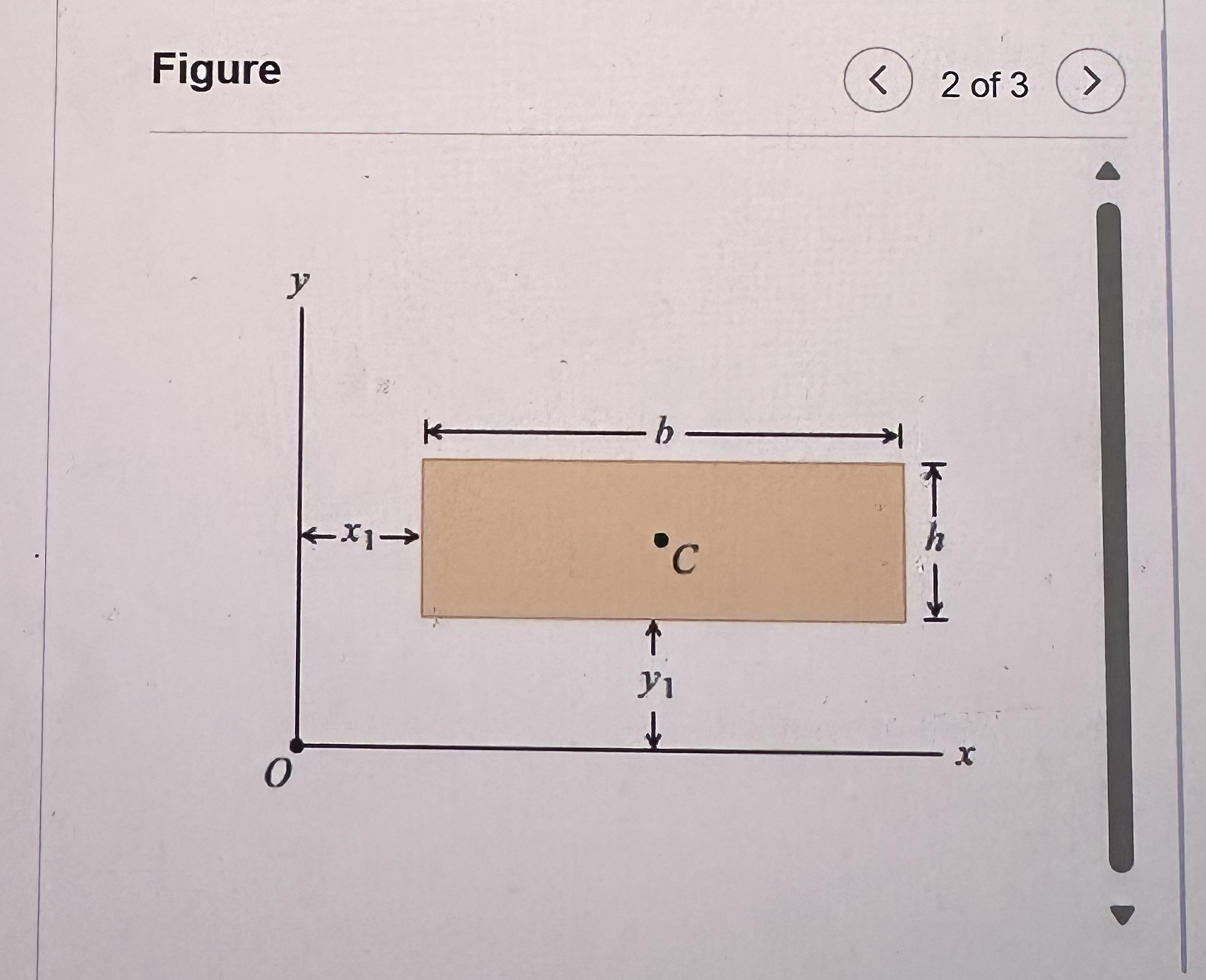
Part B

As shown, a rectangle has a base of $b=7\mathrm{.}20ft$ and a height of $h=1\mathrm{.}10ft.($Figure $2)$ The rectangle's bottom is located at a distance $y_1=2\mathrm{.}20ft$ from the $x$ axis, and the rectangle's left edge is located at a distance $x_1=3\mathrm{.}00ft$ from the $y$ axis. What are $I_x$ and $I_y,$ the area's moments of inertia, about the x and $y$ axes, respectively?

Express your answers numerically in biquadratic feet $($feet to the fourth power$)$ to three significant figures separated by a comma.

View Available Hint$($s$)$

$$

Part C

The semicircle shown $($Figure $3)$ has a moment of inertia about the $x$ axis of $51\mathrm{.}0f{t}^4$ and a moment of inertia about the $y$ axis of $51\mathrm{.}0f{t}^4.$ What is the polar moment of inertia about point $C($the centroid$)?$

Express your answer numerically in biquadratic feet $($feet to the fourth power$)$ to three significant figures.

View Available Hint$($s$)$

$$

reserved.

Terms of Use $|$ Privacy Policy.

Permissions

Contact Us

about the $y$ axis, and the polar moment of in

Figure

$2$ of $3$ertia is expressed by the following equations:

$I_x\frac{?}{b}=ar(I{)}_{x^{\text{'}}}+A{d}_y^2$

$I_y\frac{?}{b}=ar(I{)}_{y^{\text{'}}}+A{d}_x^2$

$J_O\frac{?}{b}=ar(J{)}_{C^{\text{'}}}+A{d}^2$

where $I_x$ is the area's moment of inertia about the noncentroidal $x$ axis, $\frac{?}{\text{b}\text{a}\text{r}}(I{)}_{x^{\text{'}}}$ is the moment of inertia about the centroidal $x$ axis, $A$ is the total area, $d_y$ is the perpendicular distance in the $y$ direction between the centroid and the $x$ axis, $I_y$ is the area's moment of inertia about the noncentroidal $y$ axis, $\frac{?}{\text{b}\text{a}\text{r}}(I{)}_{y^{\text{'}}}$ is the moment of inertia about the centroidal $y$ axis, $d_x$ is the perpendicular distance in the $x$ direction between the centroid and the $y$ axis, $J_O$ is the polar moment of inertia about some noncentroidal point, $\frac{?}{\text{b}\text{a}\text{r}}(J{)}_C$ is the polar moment of inertia about the centroid, and $d$ is the distance between the points $O$ and $C.$

Figure

$2$ of $3$

Figure $3$ of $3$