Question: Prove that the eigenvalues of a 2 by 2 covariance matrix E- ( are not negative. Under which conditions are both eigenvalues strictly positive?

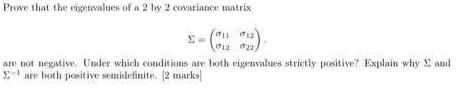
Prove that the eigenvalues of a 2 by 2 covariance matrix E-

Prove that the eigenvalues of a 2 by 2 covariance matrix E- (" are not negative. Under which conditions are both eigenvalues strictly positive? Explain why E and E- are both powitive semidefinite. (2 marks

Step by Step Solution

★★★★★

3.49 Rating (169 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Document Format (2 attachments)

63660577ca5cf_235460.pdf

180 KBs PDF File

63660577ca5cf_235460.docx

120 KBs Word File

Students Have Also Explored These Related Mathematics Questions!

Answer these questions and show your work: 1. Assume that the company that you selected for the Module 1 SLP has a bond outstanding that matures in 20 years and has a coupon rate of 6.5%. The par...

PROJECT ANALYSIS CASE One month after joining the working group of your company's investment department, planning for 2021 began and you are in the work group. You've got six projects in front of...

Answer Question 4 for some other organization, perhaps an organization where you have worked. In Question 4, Figure outlines the operations, finance/accounting, and marketing functions of three...

Match the type of mutation with it's definition the addition or removal of a nucleotide V [Choose] non functional mutation change in one nucleotide base pair extreme mutation frameshift point...

For monotone functions f, f0: P Q between posets (P, vP ) and (Q, vQ), let f v f(i) Prove that the binary relation v is a partial order. [3 marks] (ii) For monotone functions between posets p : P 0...

In this question you will be asked to reflect on a project you have been involved in or observed, in which a design evolved, or could have evolved, through applying a theory of user behaviour. You...

MATH 2350 Assignment 3 Due Wednesday March 8th at 16:00 Problem 1: Use Gram Schmidt to transform the following bases into orthonormal bases. 1 0 1 i) {0 ; 1 ; 3} . 1 1 3 1 1 1 0 2 1 2 0 ii) { 1 ; 0 ;...

Question One () Explain what is meant by an excessively volatile market? 2 Marks] ( Describe how you would test a market is "excessively volaille 15 Marks] un Explain the practical and conceptual...

answer the question clearly You are building a flight-control system for which a convincing safety case must be made. Would you assign the tasks of safety requirements engineering, test case...

You will write a program that will take an input file that describes the land, the starting point, potential lodges we can relax in, and some other characteristics for our skier. For each lodge...

The following true stresses produce the corresponding true plastic strains for a brass alloy: What true stress is necessary to produce a true plastic strain of 0.25? True Stress (psi) 30,000 60,000...

Which of the following is true of a market economy? A ) It relies on millions of individual economic decisions todetermine economic outcomes. B ) The government answers the basic economic questions...

Use the product rule to find the derivative of the given function. y = ( 2 x 4 - x 1 ) ( - x 5 2 ) y ' =

using the given letters, translate the statement into symbolic form. 1) Alaskan is sweet only if neither Heineken is balanced nor Pabst is clean tasting. Let A = Alaskan is sweet, H = Heineken is...

(3) Graph the function f(t) = t[u(t 1) u(t 3)] for t> 0, where u(t) is the unit step function, and find L[S(t)].

1) For the circuit given above find the conduction states of Diodes D1 and D2 (Vy = 0.6volts for both diodes) a) For Vs2 = 6volts b) For Vs2 = 4volts

An online Banking System that has worked successfully for XYZ Bank for the past fiveyears without any updates suddenly attracted the attention of every news outlets. Morethan half of the banks...

Consider the cash flow shown in the diagram below. What value of C makes the inflow series equivalent to the outflow series at an interest rate of 9%? $500 $300 1 21 31 51 6i 7i 81 Years 20 4.

Name: Date: PRE-LAB QUIZ 24: Are you ready to proceed? 1. Complete the table by filling in the highlighted boxes. They are in no particular order. Phylum or Clade Dominant Life Common Name Has...

In Problems 3133 A represents a 2 x 2 matrix. Use the definitions of eigenvalue and eigenvector (Section 7.3) to prove that if is an eigenvalue of A with associated eigenvector v, then - is an...

Let L - D - A denote the unnormalized Laplacian matrix for an undirected, weighted graplh G(V,8), where A is a symmetric, nonnegative adjacency matrix, and D- diag[s1,..., sv] is a diagonal matrix...

= Consider an undirected graph G = {V, E} with no isolated vertices and no self-loops. Let A be the adjacency matrix of G, and D the diagonal matrix with dii = degree(vi). Let K = D + A be the kernel...

Let AT = -A be a real, skew-symmetric n n matrix. (a) Prove that the only possible real eigenvalue of A is = 0. (b) More generally, prove that all eigenvalues of A are purely imaginary, i.e., Re ...

Let A Cmxm be hermitian. An eigenvector of A is a nonzero vector x Cm such that Ax = Ax for some A E C, the corresponding eigenvalue. %3D (a) Prove that all eigenvalues of A are real. (b) Prove that...