Please answer all parts, really struggling with these

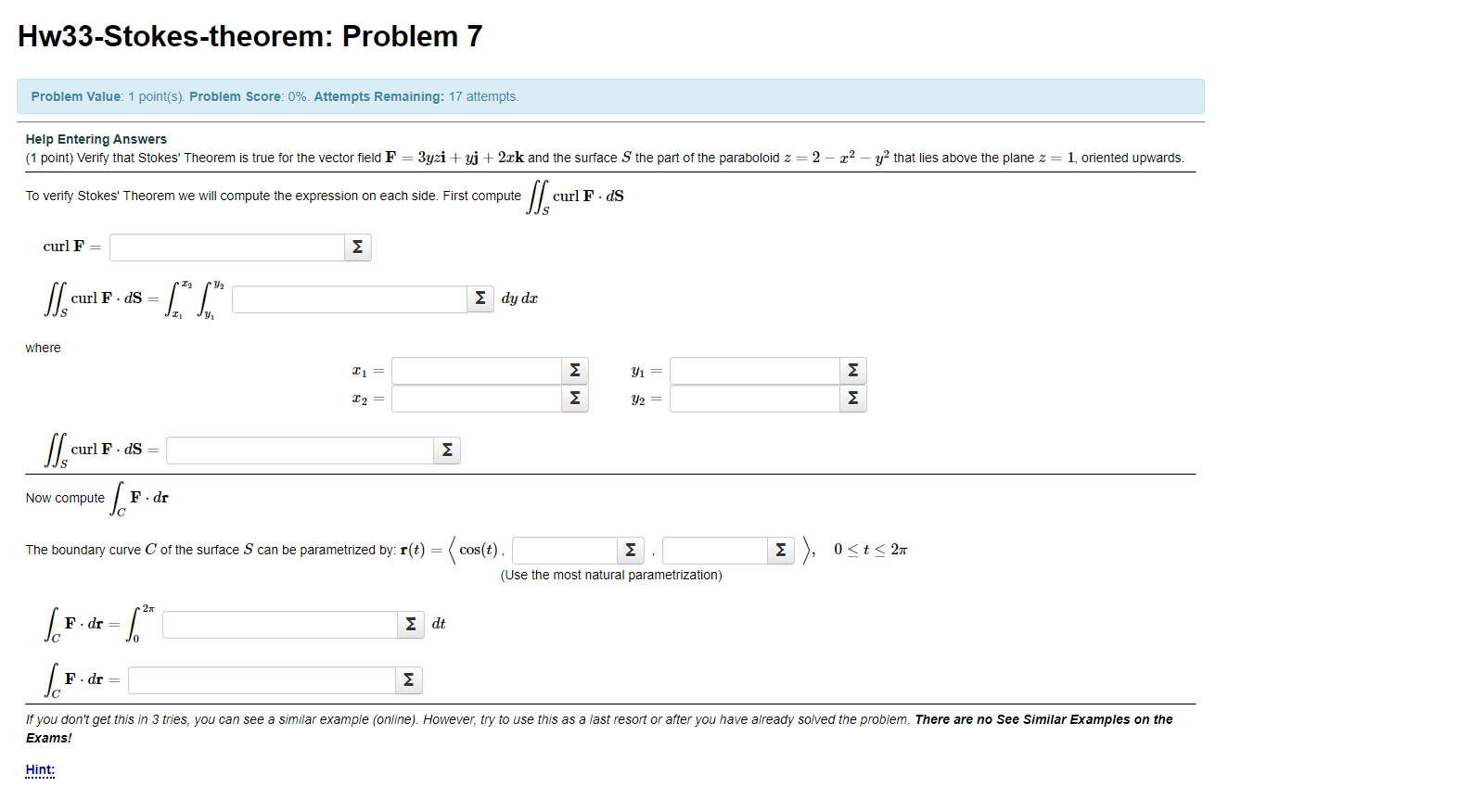
Hw33-Stokes-theorem: Problem 7 Problem Value: 1 point(s). Problem Score: 0%. Attempts Remaining: 17 attempts. Help Entering Answers (1 point) Verify that Stokes' Theorem is true for the vector field F = 3yzi + yj + 2xk and the surface S the part of the paraboloid z = 2 - x2 - y that lies above the plane z = 1, oriented upwards. To verify Stokes' Theorem we will compute the expression on each side. First compute curl F = E dy dx where T1 M y1 M TO = 92 = E Now compute F . dr The boundary curve C of the surface S can be parametrization(t) . (Use the most natural parametrization) F . dr = E dt F . de = E If you don't get this in 3 tries, you can see a similar example (online). However, try to use this as a last resort or after you have already solved the problem. There are no See Similar Examples on the Exams! Hint:F = 3 y z 8+ 4j + 2zk S : Z = 2- x2_ 42 Z = 1 Curlf = aboy /oz = 1 10 - 0)-3(2 3 4 ) + R (-32) 3 yz y 22 (a) curlF = (34-2)5-32k SS curlF. ds = S curl F. (5 x x xy) dg d x 1 - 2 2 8 ( 3 x ) + sy 2- 49 -6) dy dx - 1 -1 8 - 2 2 (b ) 24 = - 1 J1 = - VI - x2 x2 = 1 J 2 = $ 1 - x 2 (C SScurlFds = - 31 S 2 8 (t ) = 271 (F. d8 = ((- 3 sin 2t + sintcost ) dt 0 (F18 = - 371 Explaination already give Hope you got your answeres