Please answer all questions

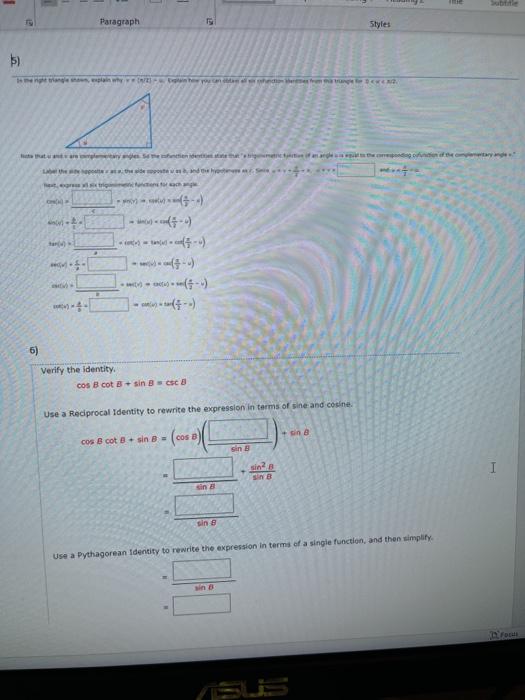
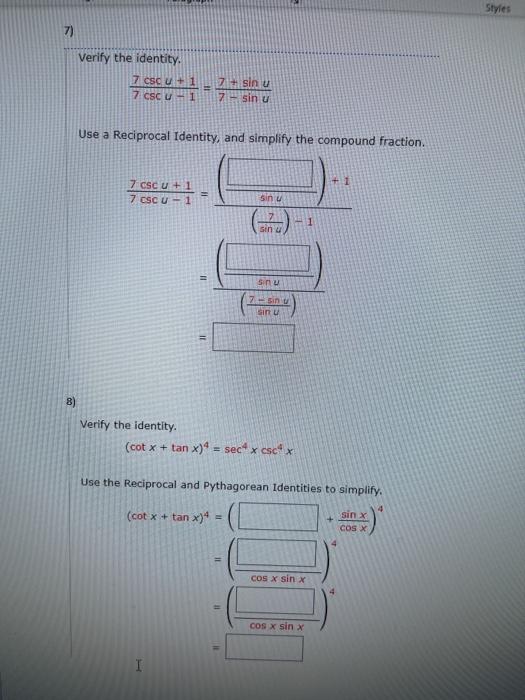
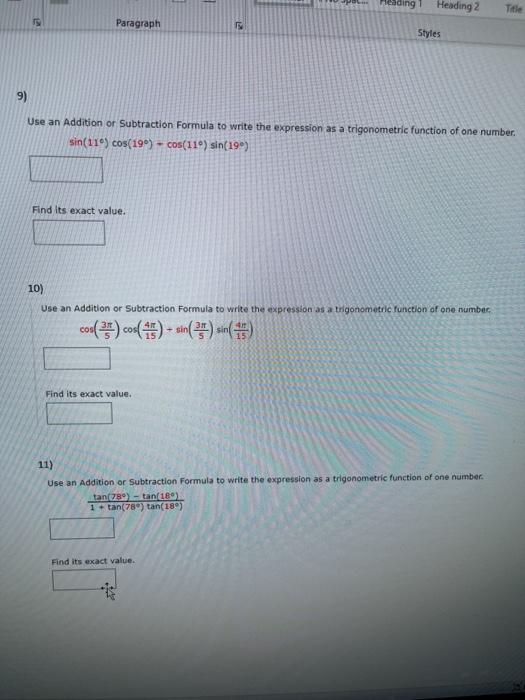
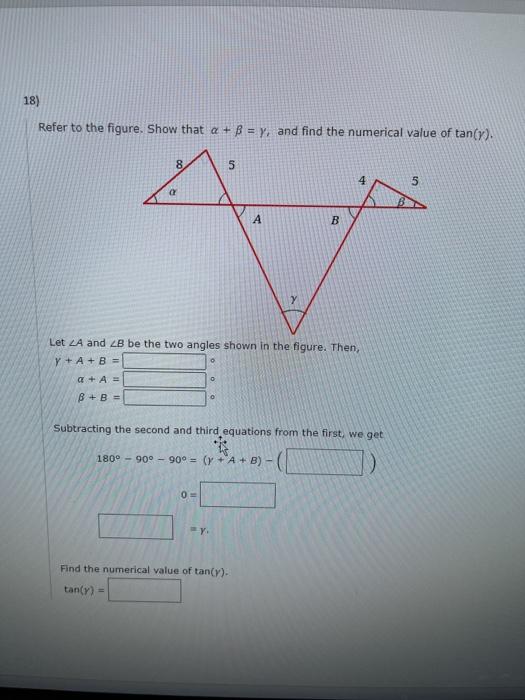
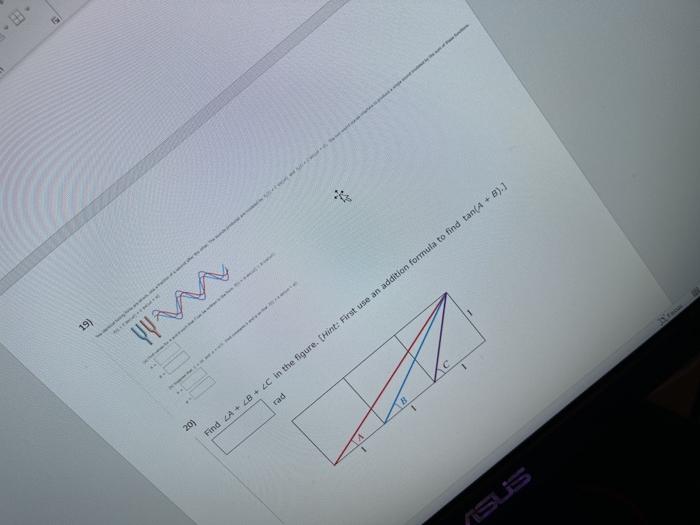
Til TO 1 Normal No Spac... Heading 1 Heading 2 Subtit Paragraph Styles 1) Verify the identity, 4 cos(x) - 2 = 2 - 4 sin?(x) 4 cos?(x) 2 = 41-( = 2 - 4 sin(x) 2) Verify the identity. sin(x) + cos(x) = 1 - sin(x) cos(x) sin(x) + cos(x) sin(x) + cos(x) (sin(x) + cos(x)) (sin?(x) - ( sin(x) + cos(x) sin(x) = cos(X) sin?(x) = sin(x) cos(x) = 1 - sin(x) cos(x) COS 3) Make the indicated trigonometric substitution in the given algebraic expression and simplify (see Example ?). Assume that 0 2. 4) Make the indicated trigonometric substitution in the given algebraic expression and simplify (see Example 7). Assume that 2. 2x = 2 sec (sec(0) + 1)(sec(0) - 1)co(@) sroon Paragraph Styles b) httle blower in der the power ---- -(-) --- 6) Verify the identity, cos B cot B + sin Besc Use a Reciprocal Identity to rewrite the expression in terms of sine and cosine. cos B cot B + sin = (cosa) sin sin e SB I sin e Use a Pythagorean identity to rewrite the expression in terms of a single function, and then simply Styles 7) Verify the identity Zlcsc u + 1 7 CSC U-1 7 sinu 7 sin u Use a Reciprocal Identity, and simplify the compound fraction. +1 7 CSC U+1 7 CSC U-1 sinu -1 sinu sinu 7 sin Sinu = 8) Verify the identity (cot x + tan x) = secx cscx Use the reciprocal and Pythagorean Identities to simplify, (cot x + tan x)" sinx cOS X = COS X sinx Cos x sinx I ding Heading 2 Title 2 Paragraph Styles 9) Use an Addition or Subtraction Formula to write the expression as a trigonometric function of one number. sin(11) cos(19) - cos(11) sin(19) Find its exact value. 10) Use an Addition or Subtraction Formula to write the expression as a trigonometric function of one number cos(***) cos(45) - sin() sin(15) Find its exact value. 11) Use an Addition or Subtraction Formula to write the expression as a trigonometric function of one number. tan(789) - tan189) 1 + tan(78) tan(189) Find its exact value. 12) prove the identity coox - 5)- so * - :) - - Use the Addition and Subtraction Formulas, and simplify. cox - 5)--(x - ) = (conc.) - (cos(x)) 1)-(-03) ( =))) - ((>(+)) - (cour)(**(=))) 1)-( 02)-(02) -(coxX+ 13) Prove the identity. 8 tan(x) - 8 tan(y) 8 sin(x- cos(x) COS() Use a Reciprocal Identity, and then rewrite as a single rational expression 8 tan(x) - 8 tan() 8 sin() Cosy) cos(x) cos(x) cos(y) Use an Addition or Subtraction Formula to simplify. 14) Find the exact value of the expression - cos tansin (3) (1) 18) Refer to the figure. Show that a + B = Y, and find the numerical value of tan(y). 8 UD 4 5 B Let A and LB be the two angles shown in the figure. Then, Y+A+B= 0 a + A B + B = O Subtracting the second and third equations from the first, we get 180 - 90 90 = (+ A + B) - 0 Find the numerical value of tan(y). tan(y) = *** 19) B 20 Find LA + 2B + 2C in the figure. (Hint: First use an addition formula to find tan(A + B). rad 15) Find the exact value of the expression. sin( cos=-(#) - tan-:() 16) Evaluate the expression under the given conditions. sin(8 - 0); tan(0) = 8 in Quadrant III, sin() 3/10 10 in Quadrant IV 17) Write the expression in terms of sine only. 3 sin(x) + 3V3 cos(fix)