please answer as many bold questions possible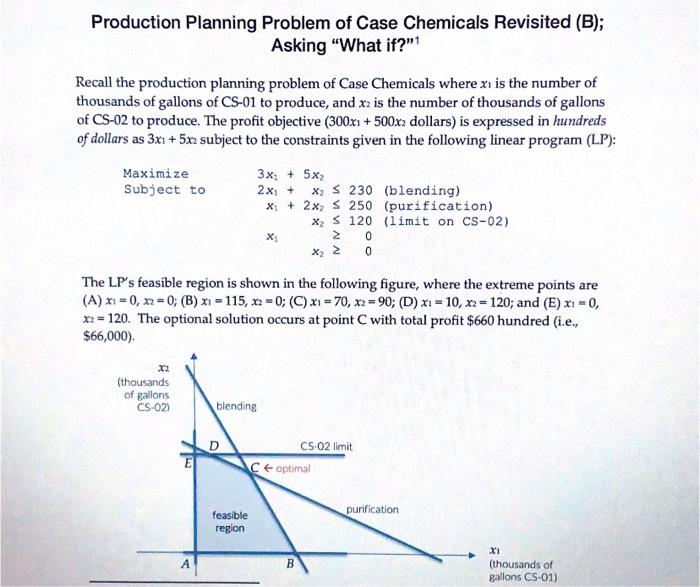

Production Planning Problem of Case Chemicals Revisited (B); Asking "What if?"1 Recall the production planning problem of Case Chemicals where x is the number of thousands of gallons of CS-01 to produce, and x2 is the number of thousands of gallons of CS-02 to produce. The profit objective (300x1 + 500x2 dollars) is expressed in hundreds of dollars as 3x + 5x3 subject to the constraints given in the following linear program (LP): Maximize 3x + 5x2 Subject to 2x + X; s 230 (blending) x + 2x S 250 (purification) X, S 120 (limit on CS-02) X X, 0 0 The LP's feasible region is shown in the following figure, where the extreme points are (A) x1 =0, x=0; (B) x1 = 115, x2 = 0; (C) x1 = 70, X2 = 90; (D) x1 = 10, x2 = 120; and (E) x1 = 0, x2 = 120. The optional solution occurs at point with total profit $660 hundred (i.e., $66,000). X2 (thousands of gallons CS-02) blending CS 02 limit Ct optimal purification feasible region B X1 (thousands of gallons CS-01) Competitor price pressure makes management uncertain if they can maintain $300 profit for every thousand gallons of CS-01 made. (They are confident in all other data.) In other words, they are uncertain of the x coefficient of 3 in the objective "maximize 3x1 + 5x.." Clearly, there is some "wiggle room for this coefficient to decrease below 3 or increase above 3 with point C(x1 - 70, x2 = 90) remaining the optimal production plan. How much wiggle room is there? If the CS-01 profit decreases too much, however, then the optimal solution will shift to point D. Similarly, if CS-01 profit increases sufficiently, then the optimal solution shifts to point B. Question 1: Report to management the smallest and largest possible coefficient for x in the objective function where point C remains the optimal solution, assuming all other data remain constant. Ignore question 1 and return to the original LP. Management is considering adding additional hours of part-time labor to obtain more weekly hours in the blending department Currently there are 230 hours available weekly. Question 2: How many dollars of additional profit would management obtain with each additional hour of blending time above 230 hours, assuming all other data remain the same? I Question 3: At some point it makes no sense to pay for additional hours of blending. What is the maximum number of labor hours (above 230 hours) that management could consider adding to the blending department each week? Ignore questions 1-3 and revert to the original LP. There is a labor shortage at Case Chemicals and the blending department is reduced to two full-time workers at 40 hours per week and one part-time worker at 30 hours per week. In other words, the weekly hours available in blending drops from 230 to 110. Question 4: What happens to the weekly profit if the blending department is reduced from 230 to 110 hours, all else the same