please answer these problems:
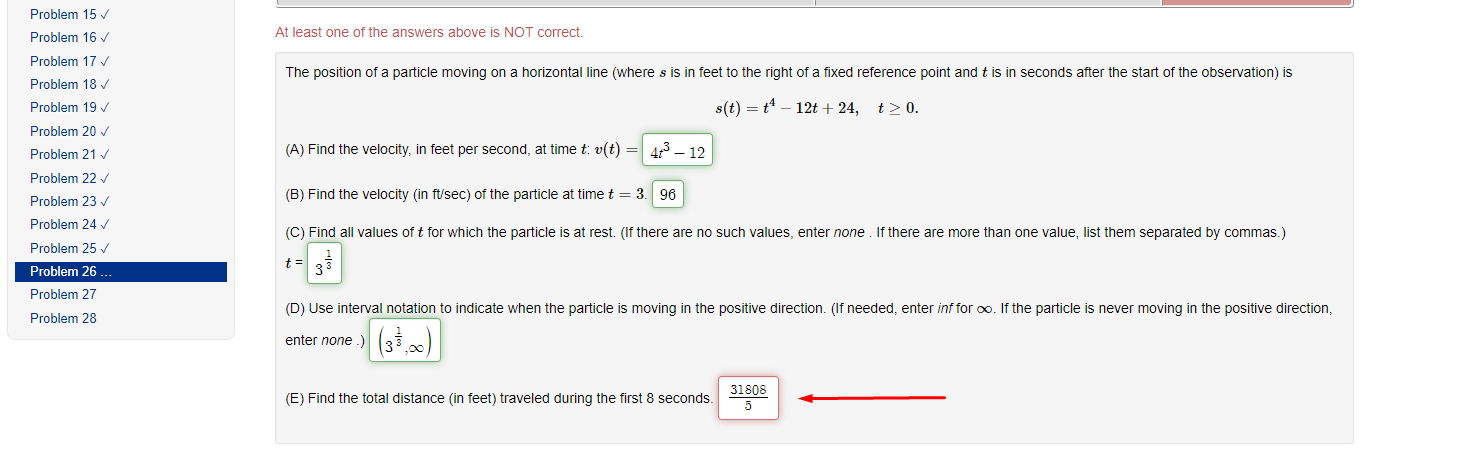
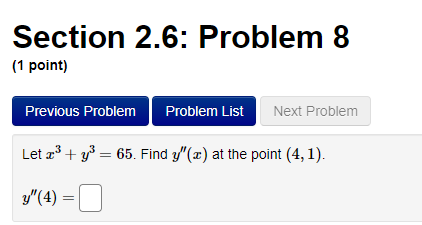
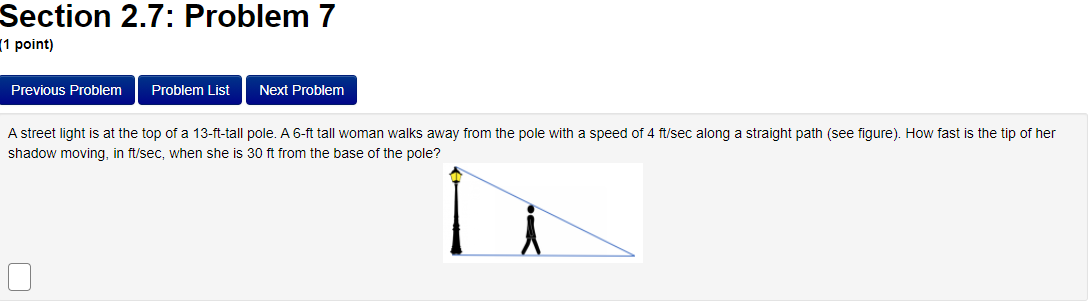
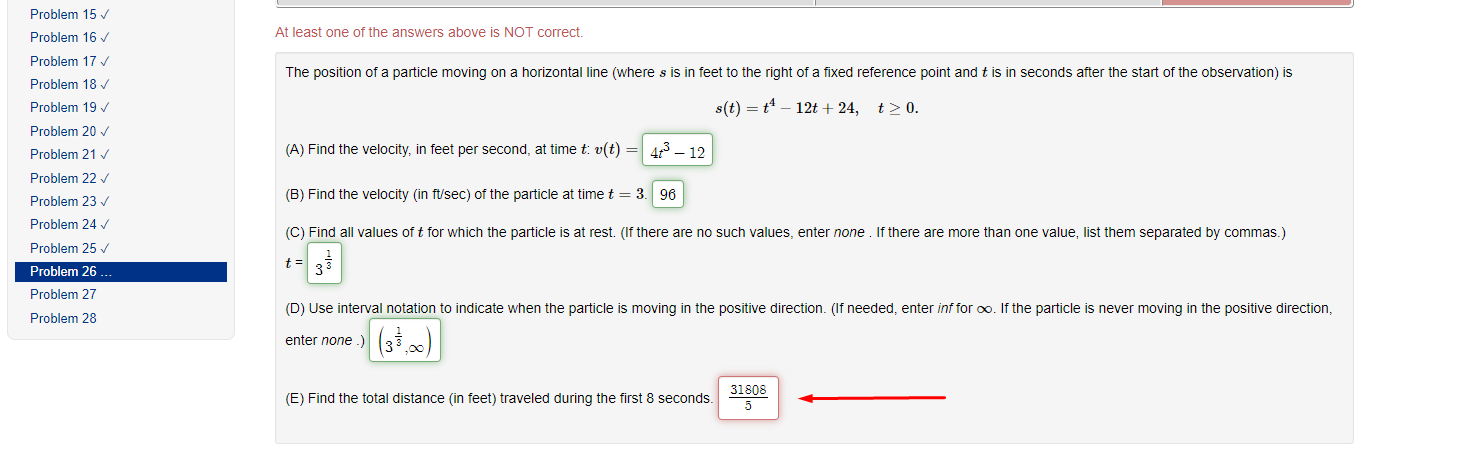
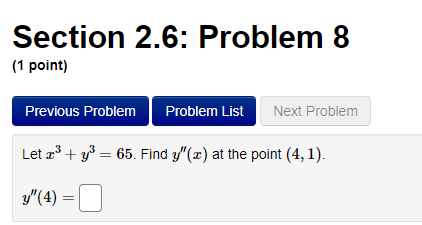
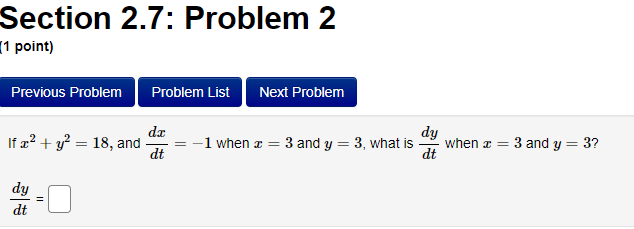
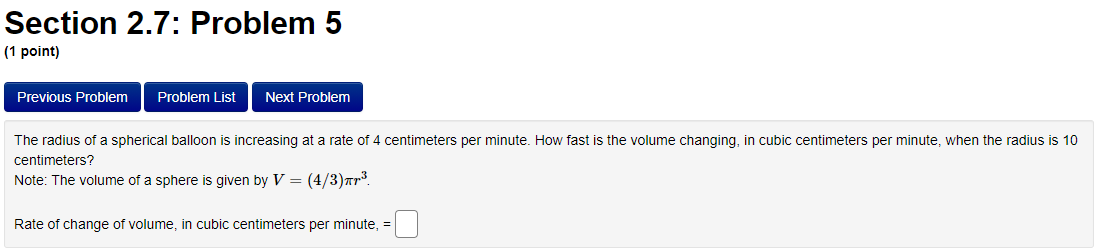
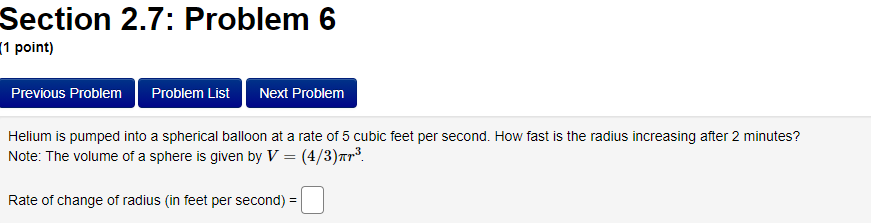
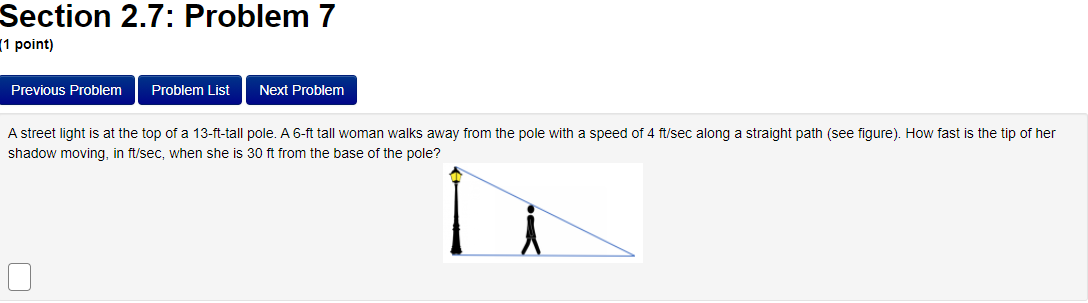
Section 2.7: Problem 1 (1 point) Previous Problem Problem List Next Problem Suppose cy = 4 and dy dx = -2. Find when c = -2. dt dt = dtProblem 15 v Problem 16 At least one of the answers above is NOT correct. Problem 17 V The position of a particle moving on a horizontal line (where s is in feet to the right of a fixed reference point and t is in seconds after the start of the observation) is Problem 18 v Problem 19 V s(t) = t* - 12t + 24, t 2 0. Problem 20 Problem 21 / (A) Find the velocity, in feet per second, at time t: v(t) = 4t - 12 Problem 22 V Problem 23 v (B) Find the velocity (in ft/sec) of the particle at time t = 3. 96 Problem 24 V (C) Find all values of t for which the particle is at rest. (If there are no such values, enter none . If there are more than one value, list them separated by commas.) Problem 25 V t = Problem 26 3 Problem 27 Problem 28 (D) Use interval notation to indicate when the particle is moving in the positive direction. (If needed, enter inf for co. If the particle is never moving in the positive direction, enter none .) (38 , 20 (E) Find the total distance (in feet) traveled during the first 8 seconds. 31808 5Section 2.5: Problem 8 (1 point) Previous Problem Problem List Next Problem Let f(x) = (7x2 -2)8(-3x2 + 8)". Then, f'(x) =Section 2.6: Problem 8 (1 point) Previous Problem Problem List Next Problem Let * + y = 65. Find y"( ) at the point (4, 1). y"(4) =Section 2.7: Problem 2 1 point) Previous Problem Problem List Next Problem If x2 + y? = 18, and dy = -1 when = = 3 and y = 3, what is when = = 3 and y = 3? dt dt dy = dtSection 2.7: Problem 3 (1 point) Previous Problem Problem List Next Problem Ify + xy - 3x = 9, and dy 2 when a = 1 and y = -4, what is dt dt when * = 1 and y = -4? = dtSection 2.7: Problem 4 1 point) Previous Problem Problem List Next Problem A particle is moving along the curve y = 2v4x + 4. As the particle passes through the point (3, 8), its -coordinate increases at a rate of 2 units per second. Find the rate of change of the distance from the particle to the origin at that instant.Section 2.7: Problem 5 (1 point) Previous Problem Problem List Next Problem The radius of a spherical balloon is increasing at a rate of 4 centimeters per minute. How fast is the volume changing, in cubic centimeters per minute, when the radius is 10 centimeters? Note: The volume of a sphere is given by V = (4/3)my3. Rate of change of volume, in cubic centimeters per minute, =Section 2.7: Problem 6 [1 point: Previous Problem Problem List Next F'roolem Helium is pumped into a spherical balloon at a rate of 5 cubic feet per second. HOW fast is the radius increasing after 2 minutes? Note: The volume ofa sphere is given by V = (all/3)\"; Rate of change of radius {in feet per second) = D Section 2.7: Problem 7 1 point) Previous Problem Problem List Next Problem A street light is at the top of a 13-ft-tall pole. A 6-ft tall woman walks away from the pole with a speed of 4 ft/sec along a straight path (see figure). How fast is the tip of her shadow moving, in ft/sec, when she is 30 ft from the base of the pole
