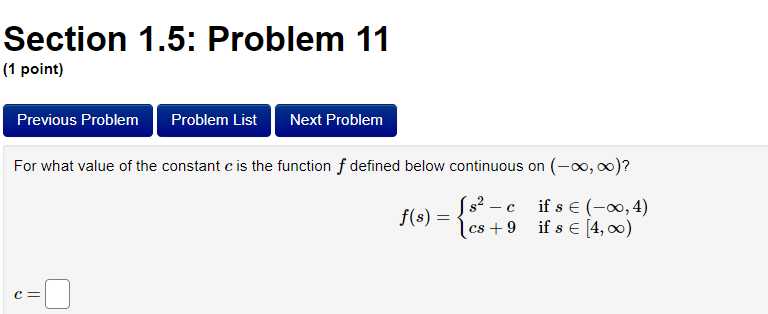
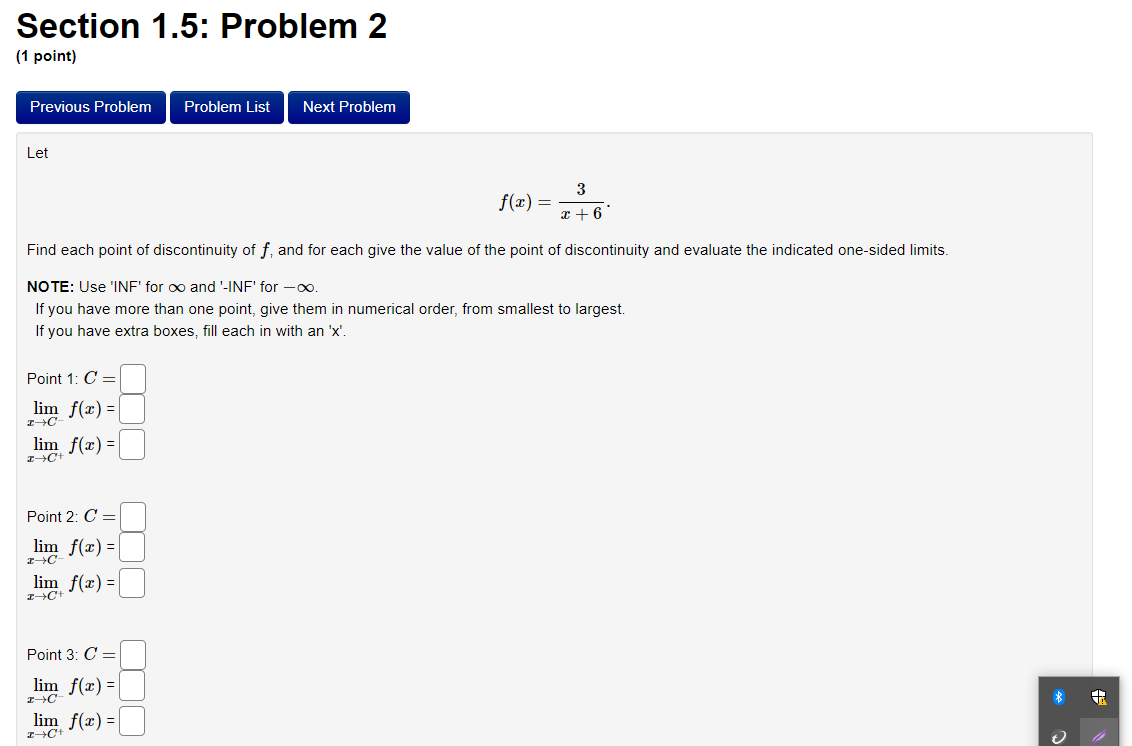
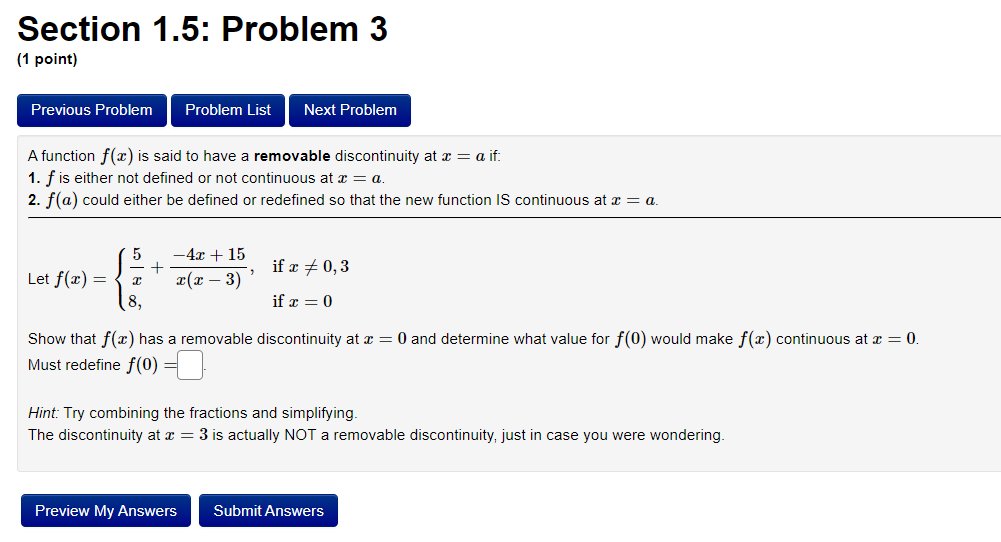
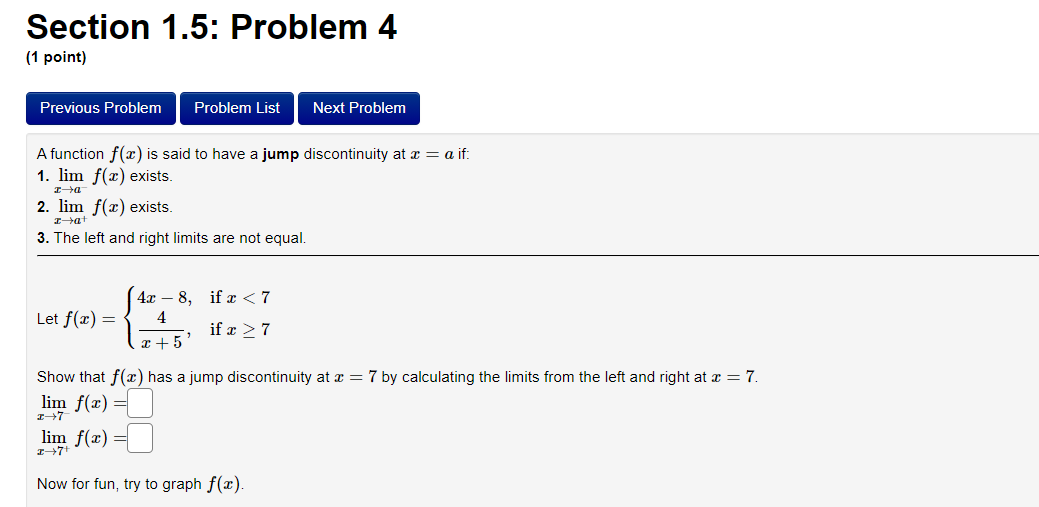
Section 1.5: Problem 1 {1 point] Previous Problem Problem List Next Problem Let 2 .1: +9 2: = . ft ) 9 _ :2 Find the points of discontinuity of f. For each of them give the number C at which the discontinuity occurs and the values of both onesided limits. Enter INF for 00, |NF for 00, DNE for does not exist, CND for cannot determine. If you nd more than one point of discontinuity, enter them in order from smallest to largest. If there are answer boxes left unlled, ll each of them with an 'x'. Point 1: C = 1% z) = 33. ne) =E] Point 2: C : 11m f{=) = zI-C' emit Point 3: C' = 1% rim) = gngz) = a Section 1.5: Problem 11 (1 point) Previous Problem Problem List Next Problem For what value of the constant c is the function f defined below continuous on (-co, co)? f (s ) = C if s E (-0o, 4) cs + 9 if s E 4, 00) C =Section 1.5: Problem 2 {1 point} Previous Problem Problem List Next Problem Let 3 z = . ) a: + 6 Find each point of discontinuity of f and for each give the value of the point of discontinuity and evaluate the indicated one-sided limits. NOTE: Use 'INF' for 00 and '|NF' for 00. If you have more than one point, give them in numerical order, from smallest to largest. Ifyou have extra boxes. ll each in with an 'x'. Point 1: C = 211% fix) _ ling fix) _ >( Point 2: C = 21% Its) _ 13:3 fix) _ Point 3: C = 21$ :12) _ ling fix) _ Section 1.5: Problem 3 (1 point) Previous Problem Problem List Next Problem A function f(a) is said to have a removable discontinuity at x = a if: 1. f is either not defined or not continuous at : = a. 2. f(a) could either be defined or redefined so that the new function IS continuous at r = a. 4x + 15 + if x 0,3 Let f(x) : r(x -3) 8. if x = 0 Show that f( ) has a removable discontinuity at a = 0 and determine what value for f(0) would make f(a) continuous at x = 0. Must redefine f(0) = Hint: Try combining the fractions and simplifying. The discontinuity at a = 3 is actually NOT a removable discontinuity, just in case you were wondering. Preview My Answers Submit AnswersSection 1.5: Problem 4 {1 point} Previous Problem Problem List Next Problem Afunction x) is said to have a jump discontinuity at :z = a if: 1. lim m] exists. Zi' 2. lim m] exists. :>a+ 3. The left and right limits are not equal. 438, if$