Please answer this question, OR Case Study.

It's one question with multiple parts.

The question is based on Operations research and involves problem solving linearly, using variables.

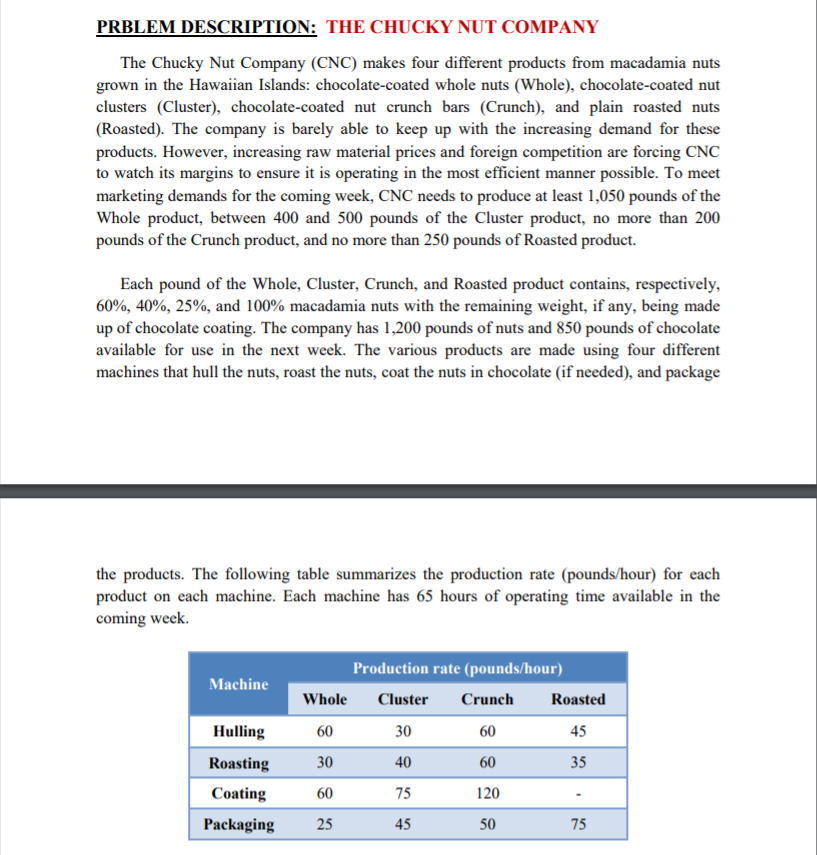
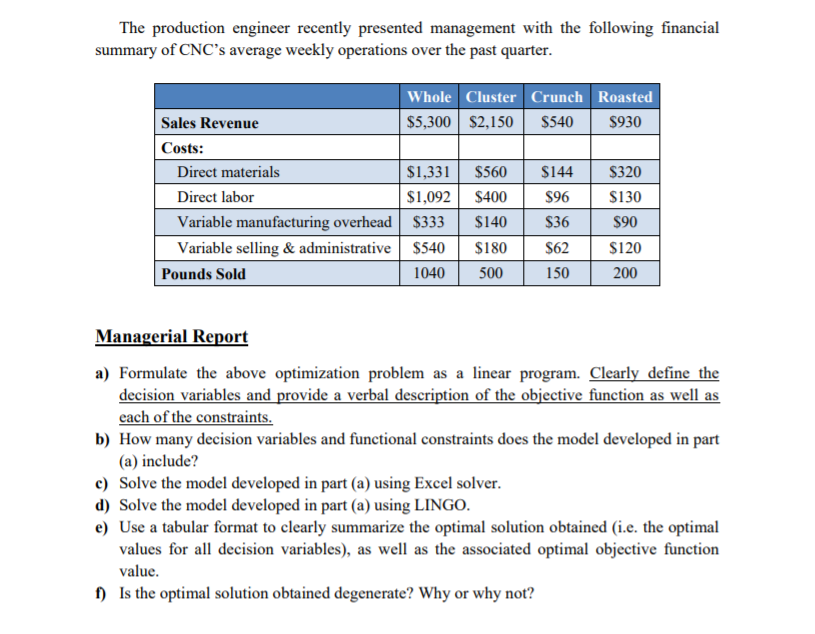
PRBLEM DESCRIPTION: THE CHUCKY NUT COMPANY The Chucky Nut Company (CNC) makes four different products from macadamia nuts grown in the Hawaiian Islands: chocolate-coated whole nuts (Whole), chocolate-coated nut clusters (Cluster), chocolate-coated nut crunch bars (Crunch), and plain roasted nuts (Roasted). The company is barely able to keep up with the increasing demand for these products. However, increasing raw material prices and foreign competition are forcing CNC to watch its margins to ensure it is operating in the most efficient manner possible. To meet marketing demands for the coming week, CNC needs to produce at least 1,050 pounds of the Whole product, between 400 and 500 pounds of the Cluster product, no more than 200 pounds of the Crunch product, and no more than 250 pounds of Roasted product. Each pound of the Whole, Cluster, Crunch, and Roasted product contains, respectively, 60%, 40%, 25%, and 100% macadamia nuts with the remaining weight, if any, being made up of chocolate coating. The company has 1,200 pounds of nuts and 850 pounds of chocolate available for use in the next week. The various products are made using four different machines that hull the nuts, roast the nuts, coat the nuts in chocolate (if needed), and package the products. The following table summarizes the production rate (pounds/hour) for each product on each machine. Each machine has 65 hours of operating time available in the coming week. Machine Production rate (pounds/hour) Whole Cluster Crunch Roasted 30 60 45 30 40 60 35 60 Hulling Roasting Coating Packaging 60 75 120 25 45 50 75 The production engineer recently presented management with the following financial summary of CNC's average weekly operations over the past quarter. Whole Cluster Crunch Roasted Sales Revenue $5,300 $2,150 S540 $930 Costs: Direct materials $1,331 $560 $144 $320 Direct labor $1,092 $400 $96 $130 Variable manufacturing overhead $333 $140 $36 $90 Variable selling & administrative $540 $180 $62 $120 Pounds Sold 1040 500 150 200 Managerial Report a) Formulate the above optimization problem as a linear program. Clearly define the decision variables and provide a verbal description of the objective function as well as each of the constraints. b) How many decision variables and functional constraints does the model developed in part (a) include? c) Solve the model developed in part (a) using Excel solver. d) Solve the model developed in part (a) using LINGO. e) Use a tabular format to clearly summarize the optimal solution obtained (i.e. the optimal values for all decision variables), as well as the associated optimal objective function value. f) Is the optimal solution obtained degenerate? Why or why not? g) Is the optimal solution obtained unique? Why or why not? h) Comment on the utilization of the resources (i.e., which of the resources have been fully utilized and which haven't). i) Comment on the range of optimality for the objective function coefficients and provide its interpretation j) Discuss the range of feasibility for the constraints right hand sides and provide its interpretation. k) Present the shadow prices for the constraints along with their interpretations. 1) If CNC wanted to decrease the production of any product, which one would you recommend and why? How much less of that product should be produced? (assume minimum production requirements could be violated). m) If CNC wanted to increase the production of any product, which one would you recommend and why? How much more of that product should be produced? (assume maximum production requirements could be violated). n) Which resource is preventing CNC from making more money? If they could acquire more of this resource, how much should they acquire & how much should they be willing to pay to acquire more of it? In case there is more than one such resource, then answer this question for each resource, one at a time. o) How much should CNC be willing to pay for every additional pound of chocolate? p) If the marketing department wanted to decrease the price of the whole product by $0.5, would the optimal solution change? Report the revised objective function value either way. q) If the marketing department wanted to increase the price of the Crunch product by $1, would the optimal solution change? Report the revised objective function value either way. r) Assuming that CNC imposes a restriction on the production quantity of Crunch whereby it shall not constitute more than 40% of the total produced from all products, how would this restriction be formulated as a constraint? Would the amendment of this constraint to the LP developed in part (a) change the optimal solution obtained earlier? Why or why not? $) Assume that the CNC has the option to run its 4 machines after hours on overtime basis for a maximum of 10 more hours per machine. The hourly rate amounts to $15, $21, $17 and $13 for the Hulling, Roasting, Coating and Packaging machines, respectively. Revisit the LP model developed in part (a) to account for overtime hours and report the revised optimal solution obtained. Which machines take advantage of the added overtime production capacity? The developed linear program(s) shall be solved using both Excel Solver as well as LINGO software. With your report, include (1) a screenshot of the Excel sheet and the Lingo codes, and (2) screenshots of the output reports generated by both Excel and Lingo after running the code, and (3) the sensitivity reports generated by both Excel and Lingo. A soft copy of the Excel and LINGO files should also be emailed to me by the above stated deadline by one of the group members. There will be NO presentations for this case