Please create math notes explaining the following math lesson and math concept in depth.

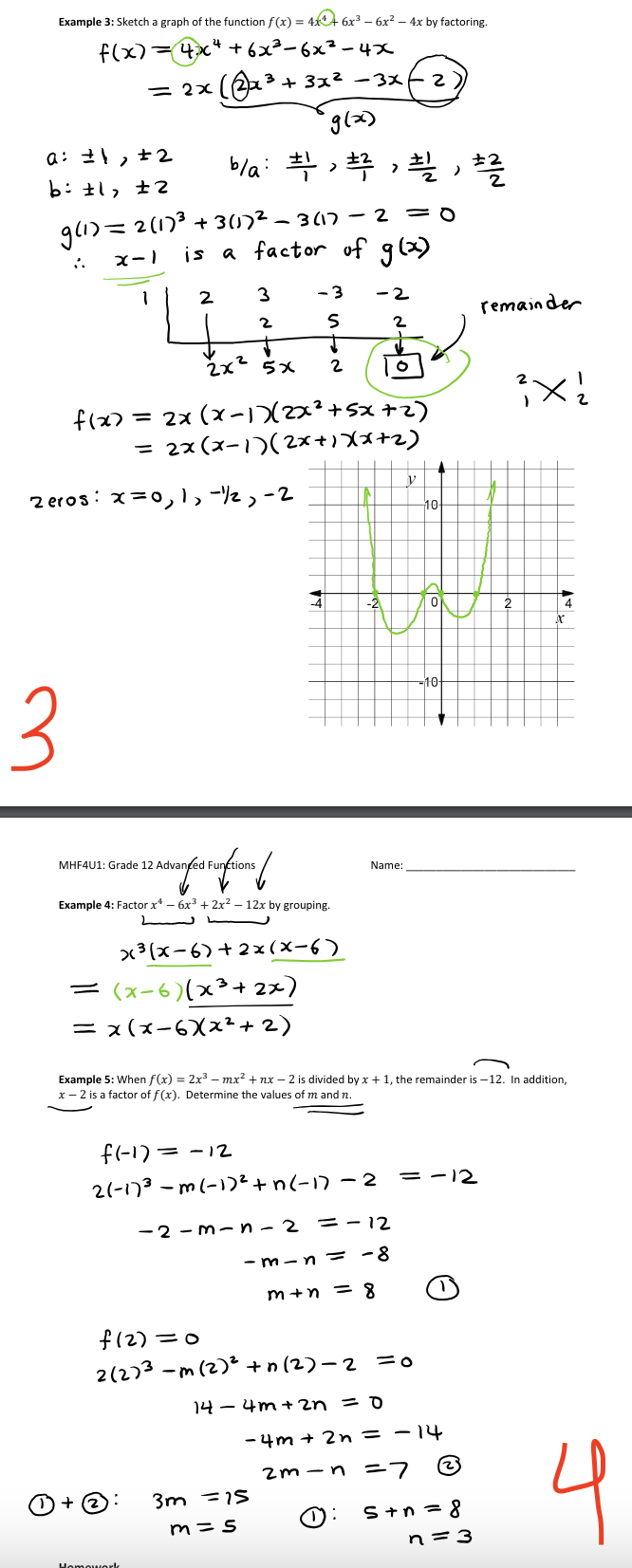
Unit 4 (Chapter 3): Polynomial Functions Lesson 4.5: Factoring Polynomials Learning Goals: To learn how to make connections between a polynomial function and its remainder when divided by a binomial (i.e., remainder theorem and factor theorem) Remainder Theorem When a polynomial, f(x), is divided by a binomial (ax - b), the remainder of this division is equal to f (b/a), where a, b E Z and a # 0. Proof: Division statement: dividend = divisor x quotient + remainder f (x) = (ax-b) x q(x) + r f ( b / a ) = 1a(b/a ) - b ) x q (b/a ) + r f ( b / a) = 0 * 9(b/ a ) +r f ( b / a ) = r Example 1: Determine the remainder when f(x) = x3 + 7x2 + 2x - 5 is divided by x + 7 by using the remainder theorem. f (-7) = (-7)3+7(-7)2+21-77-5 x - (-7) a=1 b=-7 =-19 f ( bla ) = f ( 7 ) = f (-7) MHF4U1: Grade 12 Advanced Functions Name: Factor Thegrem (ax - b) is a factor of the polynomial, f(x), if f(b/a) = 0, where a, b E Z and a # 0. Note: The factor theorem is a special case of the remainder theorem. Proof: Division statement : f ( x ) = (ax-b ) x q( x7 +r f ( x ) = (ax - b) x q(x) + o f ( b / a ) = 0 x 9(x ) +0 =o : if f( b /a ) = 0, ax - b is a factor of f ( x ) Example 2: Factor f(x) = x3 - 5x2 - 2x + 24 completely by using the factor theorem. Factor Theorem: f(x) -23- 5x2 - 2x(+ 24) (ax - b All possible factors for a: $ 1 All possible factors for b: 1 1 , +2, +3, $4, #6, +8, #12, + 24 All possible candidates for bya such that f () = 0: bla: ( #1 , $ 2 , # 3 , ".. f (1) = (170 - 5(1)2-2(1)+ 24 = 18 70 f ( 2 ) = ( 2 ) # - 5 ( 2 ) 2 - 2(27 + 24 = 8 7 0 f (-2 ) = 1-273-5(-2) 2-21-27 +24 = 0 .. x+2 is a factor of f( x) - 2 - 2 24 14 - 24 remainder 1X2 -7x 12 x-- 5x2- 2x +24 = (2+2X(202-7x+12) = (x+2xx-3)(x-4) 2Example 3: Sketch a graph of the function f(x) = 414 4 6x3 - 6x2 - 4x by factoring. f ( x ) = 4:24+6x2-6x2-4x = 2x (2 1 3 + 3x2 - 3x( 2) 9 ( x ) a: 21 , + 2 b : tl > +2 b/a: $1 , #2 , #1 , #2 9 (1) = 2(1)5 + 3(1)2 - 3(17 - 2 = 0 x - 1 is a factor of g ( 2) 2 3 - 3 - 2 2 S remainder 2x2 5x 2 O f(x) = 2x (x-17(2x2+5x+2) = 2x (x-1)(2x+)X(x+2) Zeros : x = 0, 1 , -1/2 , - 2 10 -4 2 10 W MHF4U1: Grade 12 Advanced Functions / Name: Example 4: Factor x* - 6x3 + 2x2 - 12x by grouping. x3 (x-6)+ 2x(x-6) = (x-6) ( 23+ 2x) = x (x-6)(x2+2) Example 5: When f(x) = 2x3 - mx2 + nx - 2 is divided by x + 1, the remainder is -12. In addition, x - 2 is a factor of f (x). Determine the values of m and n. f (-1) = - 12 2(-173 - m (- 1)2 + n (- 17 - 2 = - 12 - 2 - m- n - 2 = -12 - m-n = - 8 m+ n = f (2) = 0 2 ( 2)3 - m ( 2 )2 + n ( 2 ) - 2 =0 14 - 4m + 2n = 0 - 4m + 2n = -14 2m- n =7 3 1 +2 : 3m = 15 m = s O: S+n = 8 n = 3