please do not copy online

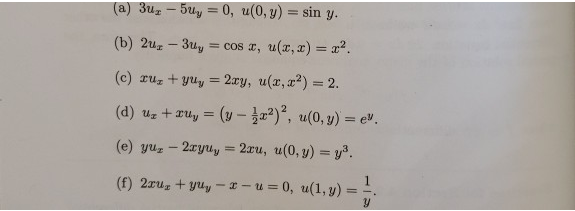
\f(a) 3ur - 5uy = 0, u(0, y) = sin y. (b) 2ur - 3uy = cost, u(x, x) = x. (c) rus + yuy = 2ry, u(x, x?) = 2. (d) ur + ruy = (y - ;x?)', u(0, y) = ev. (e) yur - 2ryuly = 2ru, u(0, y) = y3. (f) 2rus + yuy - I - u=0, u(1, y) =-Math 2300: Discrete Mathematics Turn-In Problem Set 11 The answers to the homework assignments should be your own individual work. You may discuss problems with other students in the class; however, you should not read or copy another person's solution (including internet sources). If you collaborate with other students on any of these problems, note their name at the end of your solution. Submit a pdf of your solutions to D2L Be sure to give some explanation/work, not just an answer! 1. (4 points) Find the first five terms of the sequence defined by the recurrence relation by = ba_1 - 2b,-1 + 1 for n 2 1 with the initial condition by = 3. 2. (4 points) Suppose the function g is defined recursively by g(0) = 1, g(1) = 2 and for any integers n > 1 g(n) = 3g(n - 1) - 2g(n - 2) Find g(2).g(3) and g(4). 3. (3 points each) Is the sequence [a,.] a solution of the recurrence relation on = 80,-1 - 160-2 (a) if an = 4"? (b) if an = 17 Explain your answer. 4. (4 points) Write a recursive algorithm to find the minimum of a finite list of integers, making use of the fact that the minimum of n integers is the smaller of the last integer in the list and the minimum of the first n - 1 integers in the list. Check that your code works using the list [4.5,3, 7,2, 8, 6). Use Pythontutor to check that your code does what it should. Submit a screenshot of your code and the output to the assignment dropbox on D2L