Please help

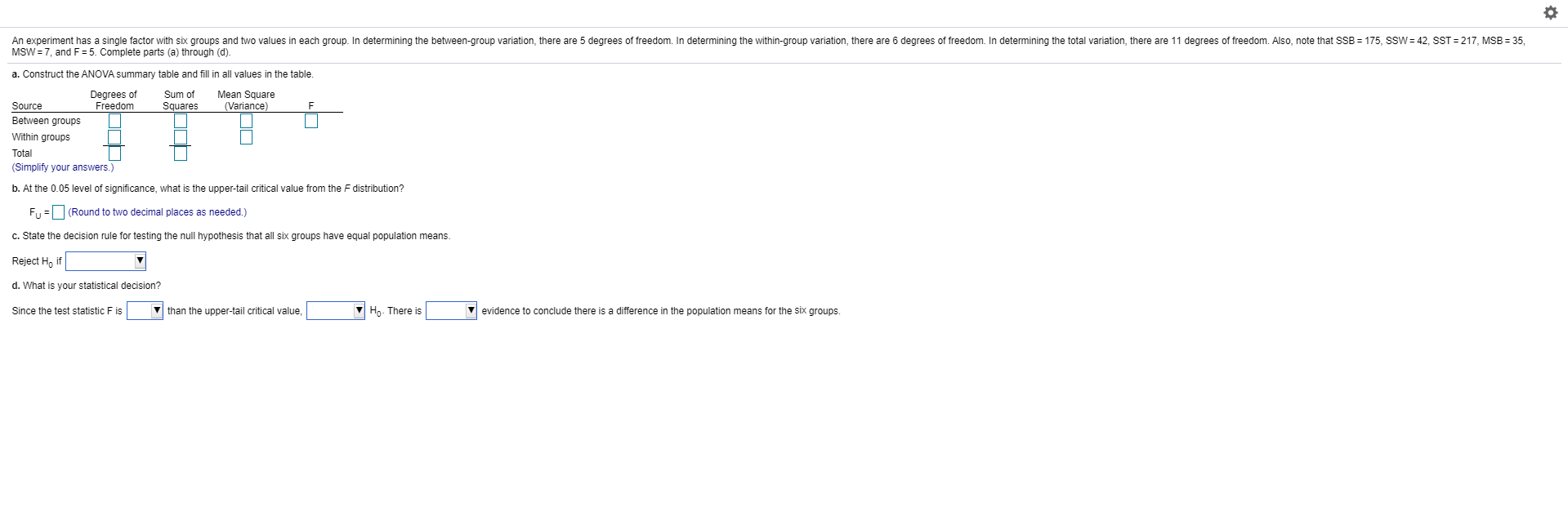
An experiment has a single factor with six groups and two values in each group. In determining the between-group variation, there are 5 degrees of freedom. In determining the within-group variation, there are 6 degrees of freedom. In determining the total variation, there are 11 degrees of freedom. Also, note that SSB = 175, SSW = 42, SST = 217, MSB = 35, MSW =7, and F = 5. Complete parts (a) through (d). a. Construct the ANOVA summary table and fill in all values in the table. Degrees of Sum of Mean Square Source Freedom Squares (Variance) Between groups Within groups Total (Simplify your answers.) b. At the 0.05 level of significance, what is the upper-tail critical value from the F distribution? Fu = (Round to two decimal places as needed.) c. State the decision rule for testing the null hypothesis that all six groups have equal population means. Reject Ho if d. What is your statistical decision? Since the test statistic F is than the upper-tail critical value, Ho- There is evidence to conclude there is a difference in the population means for the six groups