please help!

MATLAB code

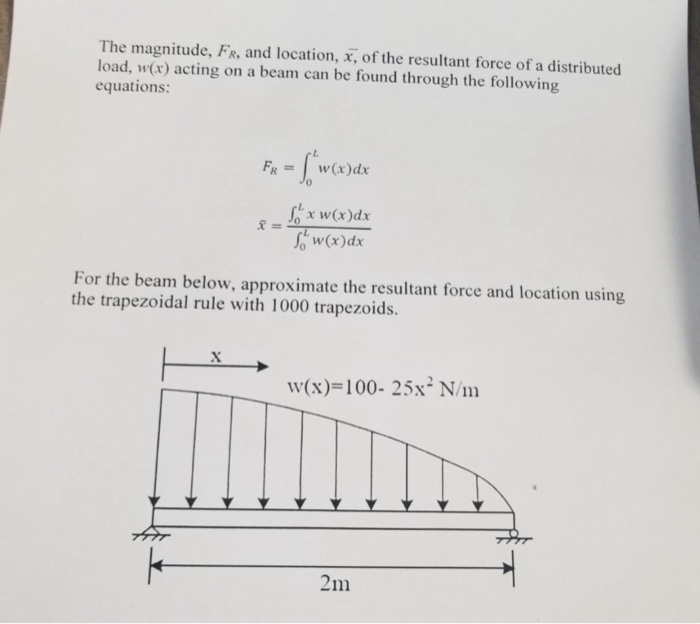
The van der Pol equation is a second order ODE given by where > 0 is a scalar parameter. We can rewrite this equation as a system of first-order ODE's by making the substitution . The resulting system of first-order ODE's is We can write the above as y f) where the bold notation means a vector. The function file below represents the van der Pol equation using. The variables n and are the entries y(1) and y(2) of a two-element vector function f deriv(t.y) Solve the ODE using the ode45 function on the time interval [0 20] with initial values [2 0]. The resulting output is a column vector of time points, t, and a solution array y. Each row in y corresponds to a time returned in the corresponding row of t. The first column of y corresponds to n and the second column to It.y]- ode45(@deriv, [0 20],12; 0]); Plot a phase plot where y(1) vs y(2) for various values of u but including ,-1. Describe the behavior as is varied. Redo the above using Euler's Method and comment on the differences The magnitude, FR, and location, x, of the resultant force of a distributed load, w(x) acting on a beam can be found through the following equations: 0 For the beam below, approximate the resultant force and location using the trapezoidal rule with 1000 trapezoids. w(x)-100- 25x N/m inl 2m