Please help me formulate this linear programming model, I am very stuck and confused!

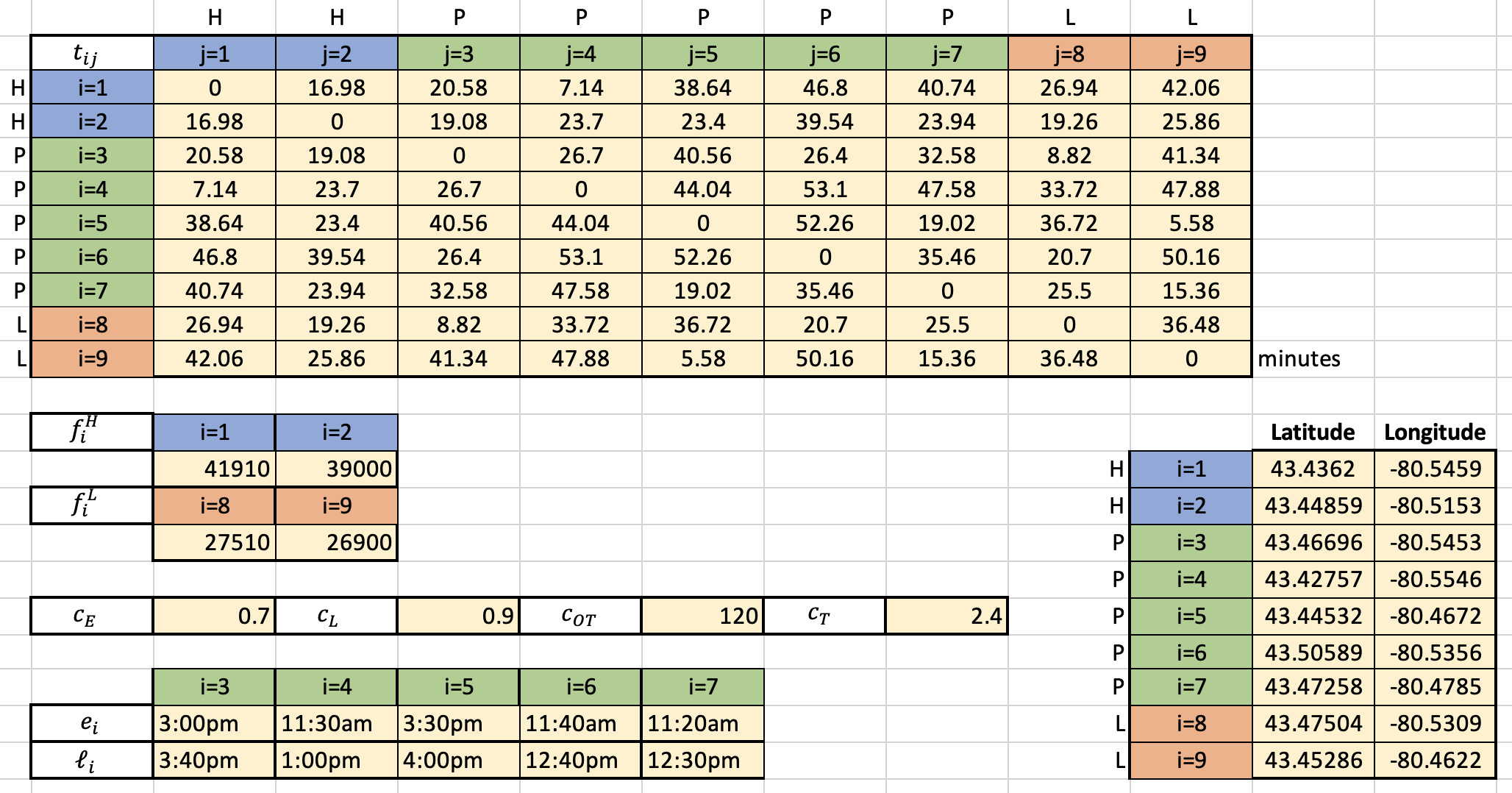
As a consequence of the current COVID-l9 crisis, Canadian Blood Services (CBS) wants to run a pilot program for setting up community-based blood collection centres in the KW region to reduce the risk to blood donors. Before launching the project, CBS has decided to establish a new clinic and a laboratory to serve this region. Each day, a nurse will start his/her trip from the new clinic and visit each of the community centres one-by-one to collect blood. At the end of the day, s/he will return all of the collected blood to the new laboratory for testing. CBS has determined a set of candidate locations for the new clinic and the new laboratory, and is asking you to help them select the best location for each of these facilities and the optimal schedule for the nurse such that the total cost is minimized. A pilot dataset including information of 5 community centres in the KW area is provided to be used in this project. The time horizon being considered for the project is 1 year (365 days). Problem Description: Let the set of candidate locations for the clinic and the lab be denoted by H = {1,2} and L = {8,9}, respectively. The yearly xed cost of opening a clinic at location i E {1,2} is fly, and the yearly xed cost for opening a laboratory at location i E {8, 9} is f f . Let the set of community centres be denoted by the set P = {3, 4, 5, 6, 7}. It is known that sets H, L and P are disjoint sets (there are no overlaps in their locations). Let ti- denote the parameter for the time required to go from any location i E {1, 9} to any location j E 1 {1, 9} in minutes (from/to locations can be from any of the sets H, L, P).* Assume that the travel cost is CT per minute. All registered community centres (i E P) must be visited by the nurse before the nurse goes to the laboratory. Assume that the same set of community centres should be visited every single day (365 days) of the year, i.e., the nurse will complete his/her daily trip 365 times in a year. Each community centre requests a specic time window for the arrival of the nurse. Let eil and 31-1 represent the earliest and latest arrival time preferred by the community centre located at location i E P. Violation of these time window requirements will cause CBS to incur a penalty cost of CE per minute for early arrival and CL per minute for late arrival. Assume the nurse spends 30 minutes at each community centre. The regular working hours of the nurse are 8am to 4pm. If necessary, he/ she can work overtime after 4pm, which will cost CBS an additional COT per hour. Formulate and solve a mathematical programming model to nd the optimal location of the new clinic and the laboratory as well as the optimal route (starting from the clinic and ending at the laboratory) and schedule (what time each community centre is visited) of the nurse such that all the requirements above are explicitly taken into account. The goal is to minimize total cost including the xed cost of locating facilities as well as the annual cost for overtime, travel, and the penalty for time-window violation. \f