Question: please help me! Given a positive constant b, here are the parametric equations of a spiral curve passing through the point (1,0) and a graph
please help me!
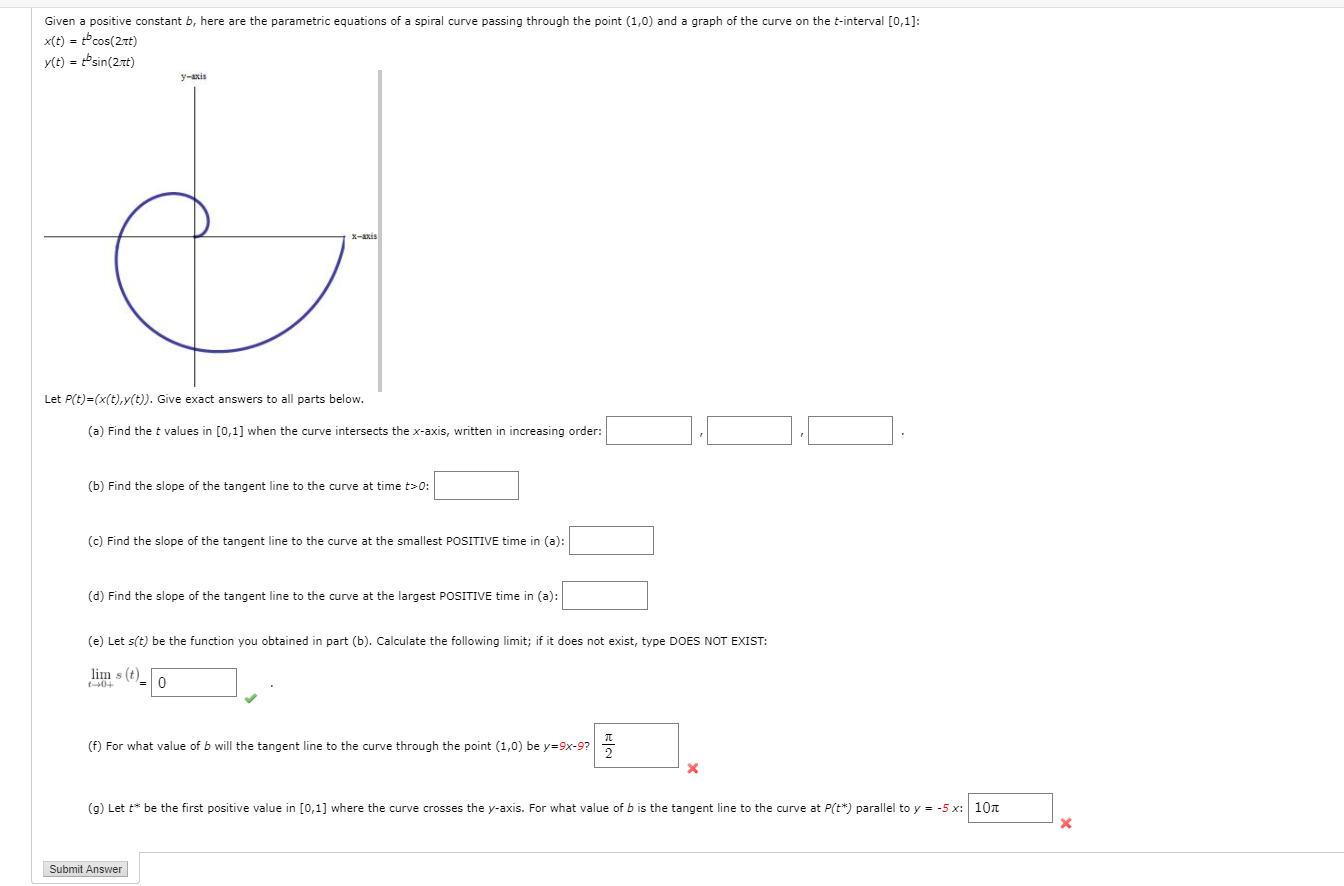
![graph of the curve on the t-interval [0,1]: x(t) = tcos(2nt) y(t)](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/questions/2024/11/672f6b2729778_870672f6b2701b78.jpg)
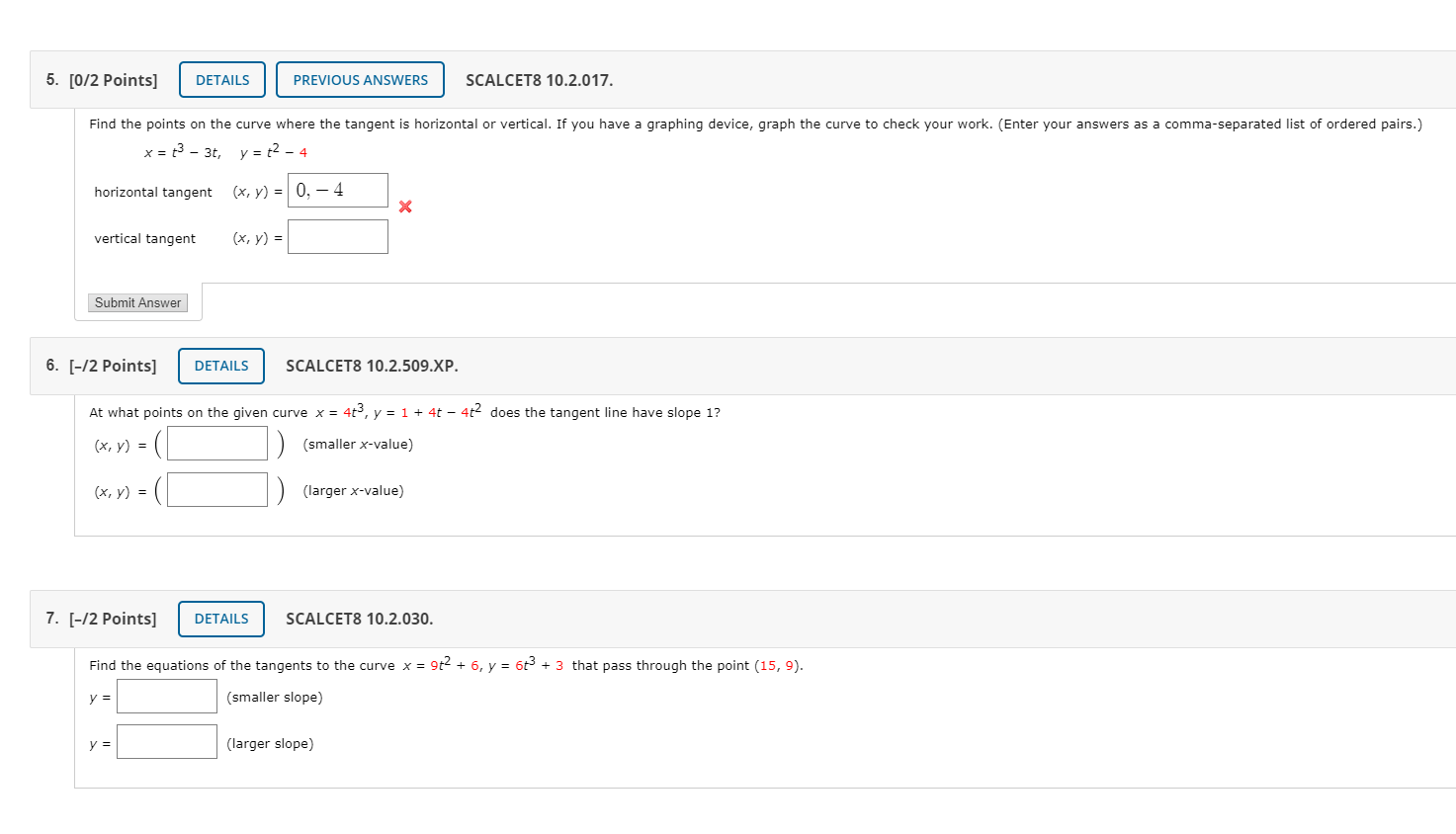
![(a) Find the t values in [0,1] when the curve intersects the](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/questions/2024/11/672f6b2a458f9_874672f6b2a12799.jpg)
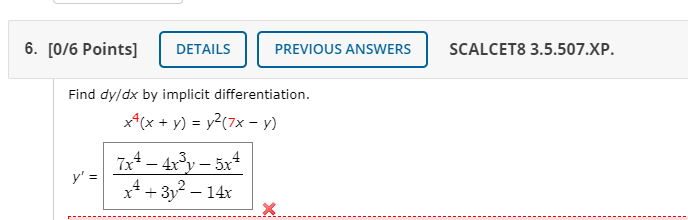
Given a positive constant b, here are the parametric equations of a spiral curve passing through the point (1,0) and a graph of the curve on the t-interval [0,1]: x(t) = tcos(2nt) y(t) = tosin(2nt) y-axis Let P(t)=(x(t),y(t)). Give exact answers to all parts below. (a) Find the t values in [0,1] when the curve intersects the x-axis, written in increasing order: (b) Find the slope of the tangent line to the curve at time t> 0: (c) Find the slope of the tangent line to the curve at the smallest POSITIVE time in (a): (d) Find the slope of the tangent line to the curve at the largest POSITIVE time in (a): (e) Let s(t) be the function you obtained in part (b). Calculate the following limit; if it does not exist, type DOES NOT EXIST: lim s (t)= 0 (f) For what value of b will the tangent line to the curve through the point (1,0) be y=9x-9? (g) Let t* be the first positive value in [0,1] where the curve crosses the y-axis. For what value of b is the tangent line to the curve at P(t*) parallel to y = -5 x: 10n X Submit Answer5. [0/2 Points] DETAILS PREVIOUS ANSWERS SCALCET8 10.2.017. Find the points on the curve where the tangent is horizontal or vertical. If you have a graphing device, graph the curve to check your work. (Enter your answers as a comma-separated list of ordered pairs.) x = t3 - 3t, y = t2 - 4 horizontal tangent (x, y) = 0, - 4 X vertical tangent ( x, y ) = Submit Answer 6. [-/2 Points] DETAILS SCALCET8 10.2.509.XP. At what points on the given curve x = 4t3, y = 1 + 4t - 4t2 does the tangent line have slope 1? ( x, y ) = (smaller x-value) ( x, y ) = (larger x-value) 7. [-/2 Points] DETAILS SCALCET8 10.2.030. Find the equations of the tangents to the curve x = 9t2 + 6, y = 6+ + 3 that pass through the point (15, 9). y : (smaller slope) larger slope)To nd g? = y' for x? + y = S, we differentiate both sides of the equation with respect to x. cm the right-hand side, we have the following. i _ 3 l K On the lefthand side, we have %[x? + 1.44]. We already know that 0%[1'4] = 4y3y'. For the term x]: we have the following. d _ 6 -x \f3. [-/6 Points] DETAILS SCALCET8 3.5.501.XP. Consider the following. + +1 = 2 (a) Find y' by implicit differentiation. V' = (b) Solve the equation explicitly for y and differentiate to get y' in terms of x. y'= (c) Check that your solutions to part (a) and (b) are consistent by substituting the expression for y into your solution for part (a). y' = 4. [-/6 Points] DETAILS SCALCET8 3.5.503.XP.MI. Find dy/dx by implicit differentiation. x8 + y = 5 y'
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


