Please help me solve question 3! ! The second and the third pictures are the answers to the first question and the second question respectively.

1.

2.

3.

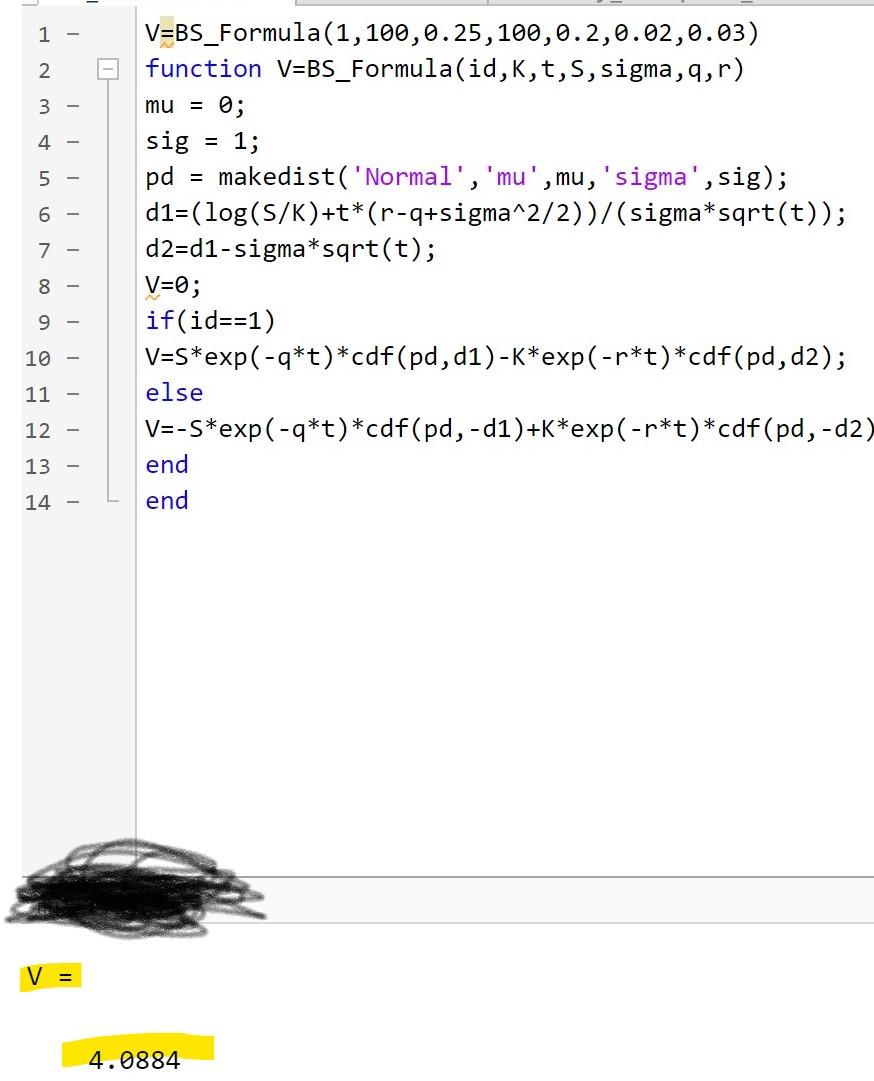
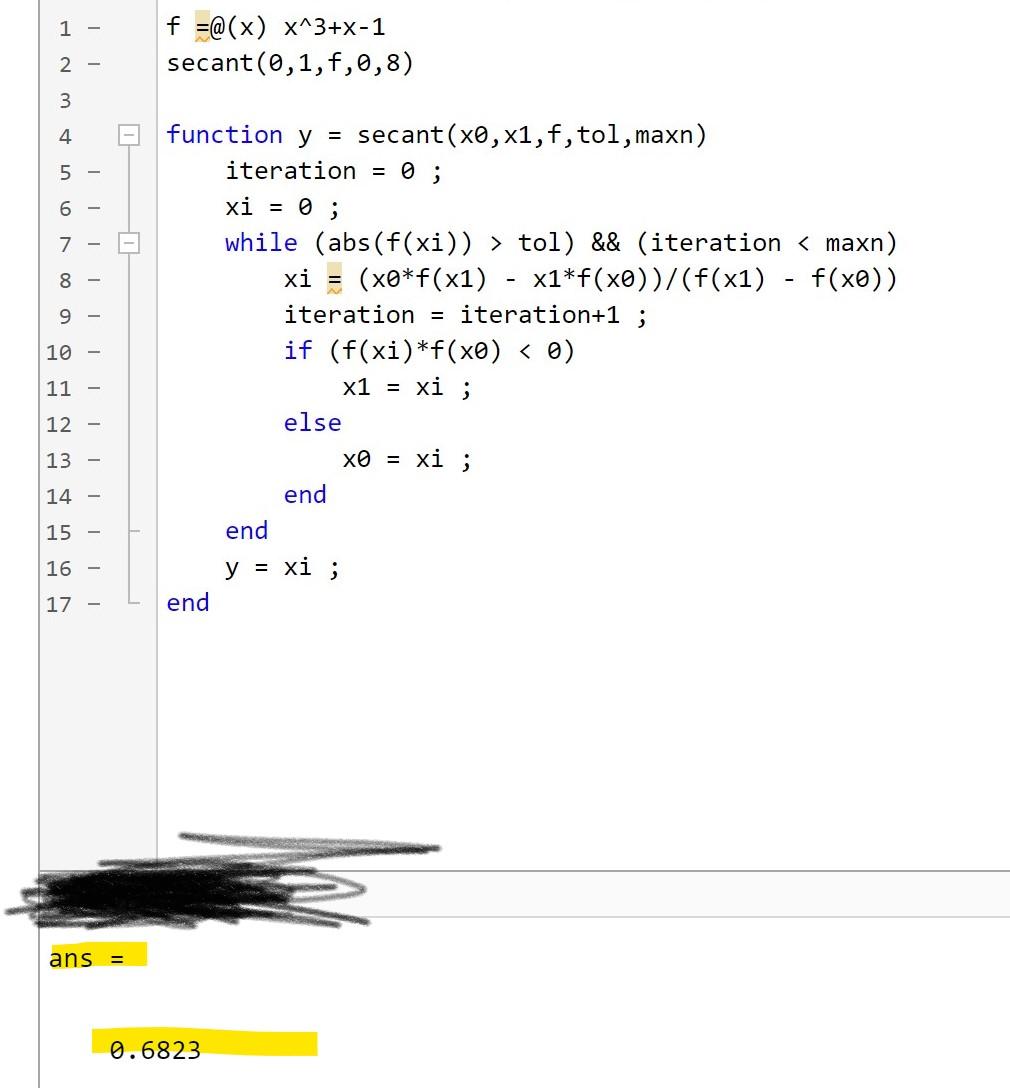
Project 1: Nonlinear Solvers and Implied Volatility 1. We solve a nonlinear equation f(x) = 0. Write a MATLAB function for secant method. function y = secant (x0, x1,f, tol,maxn) x0,x1 are two initial guesses. f is the function handle. For example, f=Q(x) x*x+x+1. tol is the tolerance regarding the stopping criteria. Use the absolute error. maxn is the maximum number of iterations allowed for the algorithm. To test your program, call the function with the following inputs: f(x) = x + x -1, Co= 0, 1 = 1. After 8 iterations, xg shall be obtained as 0.68232780382802. 2. The Black-Scholes formulas consist of C = Se-qf Nd) - KertN(d2), P= Ke-rtN(-d2) - Se-9 N(-d), where In(S/K) +t(r - 9 +9+02/2) di = d2 = d-ovi. ovt In the above, o is the implied volatility and N(2) is the cdf of a standard normal random variable. Write a MATLAB function to compute the Black-Scholes formulas. function V = BS_Formula(id, K, t, S, sigma, q, r) To calculate N(x) in the formula, use the intrinsic MATLAB function cdf. If id==1, the function is for a call option. Otherwise it is for a put option. We use the following parameters to test: K = 100, S= 100, r=0.03, t = 0.25, o=0.2, q=0.02, which shall yield following approximations C4.0884, P-3.8399 3. In Problem 2, we can compute an option price, V, given an implied volatility, o. In this problem, we compute a given V. Write a MATLAB function to compute the implied volatility of an option under the Black-Scholes model using the secant method. function sigma volatility_european_formula(id, V, K, t, S, q, r, ... so, s1, tol, maxn) V is the option price, and so and s1 are two initial values. 1 - f =@(x) x^3+x-1 secant(0,1,f,0,8) 2 - 3 4 5 - 6 - 7 - 8 - 9 - 10 - function y = secant(x0, x1, f, tol, maxn) iteration 0; xi = 0; while (abs(f(xi)) > tol) && (iteration tol) && (iteration