Please help with all problems.

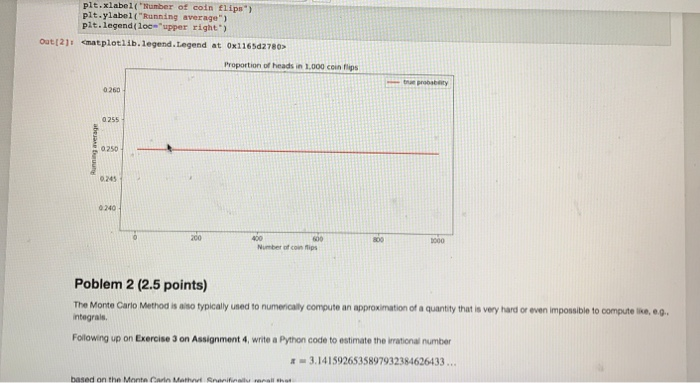
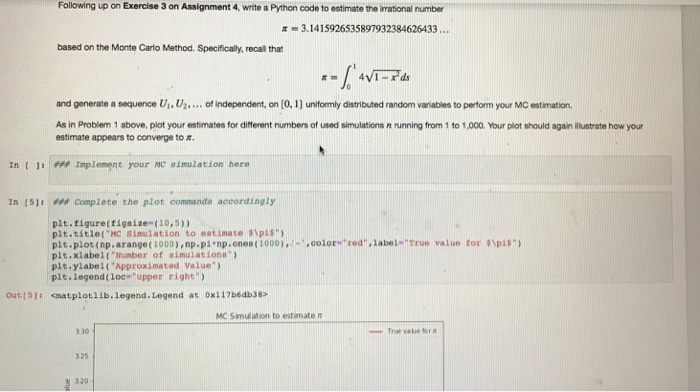
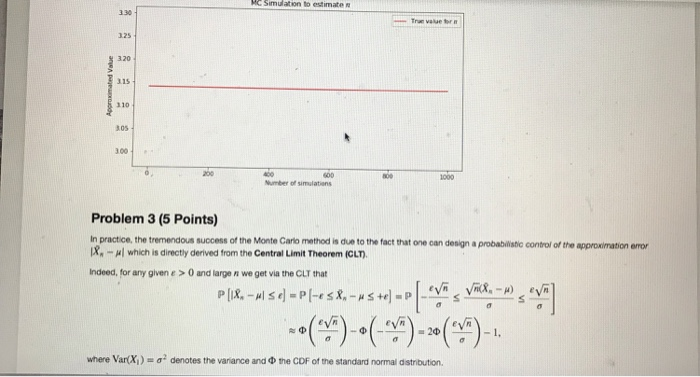
The Monte Carto Method (Monte Carlo Simulation) was first published in 1949 by Nicholas Metropolis and Stanislaw Ulam in the work "The Monte Carlo Method" in the Journal of American Statistics Association. The name Monte Cario has its origins in the fact that Ulam had an uncle who regularly gambled at the Monte Carlo casino in Monaco. In fact, way before 1949 the method had already been extensively used as a secret project of the U.S. Defense Department during the so-caled "Manhattan Project The basic principle of the Monte Carlo Method is to implement on a computer the Strong Law of Large Numbers (SLLN) If we can generate a sequence , , X2-.. of Li d. random variables (e . independent and identically distributed with finte mean EX, ] SLLN guarantees that the sample mean (or empirical mean , then the 14o with probability 1. Xi +x,+ + x,-. as n In other words, X, is a good approximation for u if the number of simulations n is large enough: 8, ~ for n large, In addition, if we are interested in approximating the probablity that some event A occurs, we might adopt the SLLN as folows: We simulate repeated ndependent trials of a random experiment and define the sequence of random variales X.X...vl ,.{O if A occurs on the i-th simulation ifA does not occur on the i-th simulation 1 ifA does not occur on the ulat simulation (i-1.23 ) 0 Then, R, is the proportion of the n triais in which A occurs. By construction the random varables Xx,.X... are independent and identicaly dstributed with mean E[%).PlA]. Thus, by the SLLN we again obtain xi +X2 + + X.-PAI - P[A] with probability 1. as n as n and hence ,PIA for n large