Please i need help with this C programming question :

Write a C program that calculates various formulas converging towards nombre ?(Pi) to compare these formulas convergence rate. Each formula will be calculated by a different function. Each function will have the same parameter that indicates the number of terms to be used in the formula to approximate the value of number. Here are the formulas that your program must calculate, in order of convergence rate of the slowest to fastest :

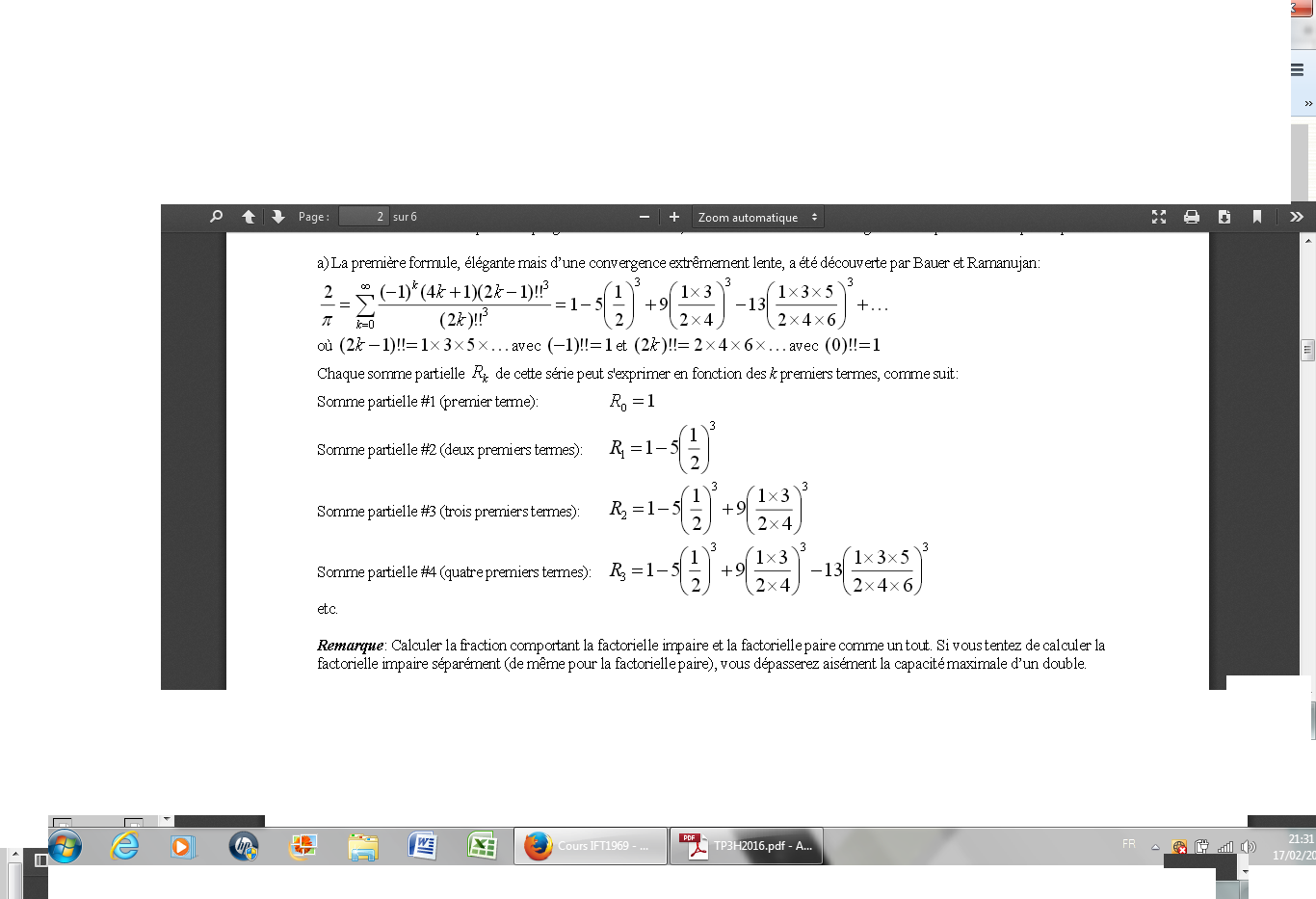
a) The first formula, elegant but extremely slow convergence, was discovered by Bauer and Ramanujan:

where with and with

Each partial sum of this series can be expressed in terms of k terms, as follows:

Partial sum#1 (first term):

Partial sum#2 (first two terms):

Partial sum#3 (first three terms):

Partial sum#4 (first foor terms):

etc.

Note: Calculate a fraction with odd factor and the factor pair as a whole. If you try to calculate the odd factor separately (the same for the factorial pair), you easily will exceed the maximum capacity of a double.

b) The second formula, of great simplicity with a very slow convergence, was discovered by Leonhard Euler:

Each partial sum of this series can be expressed in terms of the first k terms, as follows:

Partial sum#1 (first term):

Partial sum#2 (first two terms):

Partial sum#3 (first three terms):

Partial sum#4 (first foor terms):

etc.

c) The third formula, with a relatively rapid convergence, has been discovered by Sharp:

Each partial sum of this series can be expressed in terms of the first k terms, as follows:

Partial sum#1 (first term):

Partial sum#2 (first two terms):

Partial sum#3 (first three terms):

Partial sum#4 (first foor terms):

etc.

d) The last formula, very elegant and with the author's name is unknown, is expressed as a fraction continues; in addition, it converges rather quickly:

Each partial fraction of this continued fraction can be expressed in terms of the first k terms, as follows:

Partial Fraction # 1 (first term) :

Partial Fraction # 2 (first two terms) :

Partial Fraction # 3 (first three terms) :

Partial Fraction # 4 (firstfoor terms) :

etc.

Note : Small suggestion to calculate this continued fraction, start with the last term, and then continue with the second last term, and so on.

Here are partial results for the expected outputs in your program:

Convergence PI calculation with Bauer-Ramanujan's formula

Value with 1 terms = 2.0000, error = 1.1416

Value with 3 terms = 2.3540, error = 0.7876

Value with 7 terms = 2.5825, error = 0.5591

Value with 15 terms = 2.7394, error = 0.4022

Value with 31 terms = 2.8515, error = 0.2901

Value with 63 terms = 2.9327, error = 0.2089

etc.

Convergence PI calculation with Euler's formula :

Value with 1 terms = 2.8284, error = 03132

Value with 3 terms = 3.0346, error = 0.1070

Value with 7 terms = 3.0959, error = 0.0457

Value with 11 terms = 3.1125, error = 0.0291

Value with 19 terms = 3.1248, error = 0.0168

Value with 35 terms = 3.1325, error =0.0091

etc.

Convergence PI calculation with the formula of Sharp

Value with 1 terms = 3.46410161513775, error =0.32250896154796

Value with 3 terms = 3.15618147156995, error =0.01458881798016

Value with 5 terms = 3.14260474566308, error =0.00101209207329

Value with 7 terms = 3.14167431269884, error =0.00008165910904

Value with 9 terms = 3.14159977381151, error =0.00000712022171

Value with 11 terms = 3.14159330450308, error =0.00000065091329

etc.

Convergence PI calculation with the continued fraction formula

Value with 1 terms = 3.00000000000000, error =0.14159265358979

Value with 3 terms = 3.13725490196078, error =0.00433775162901

Value with 5 terms = 3.14146341463415, error =0.00012923895565

Value with 7 terms = 3.14158882509212, error =0.00000382849767

Value with 9 terms = 3.14159254044654, error =0.00000011314325

Value with 11 terms = 3.14159330450308, error =0.00000000333955

etc.

Note1 : -You will find that the values calculated by the program using a number of terms that are not consecutive (for example, with the first formula of Bauer and Ramanujan, use one term, then 3 terms and terms 7, etc.). This irregularity can be explained by the algorithm used to determine the number of terms to calculate. Is to calculate one term and define a increment (an integer variable) set to 1 (as if we wanted to use 2 terms in the second loop, then three terms in the third iteration, etc.); calculating the absolute error of the current iteration and is compared with the absolute error of the iteration Previous: If this comparison reveals that no new significant figure appeared, doubling the increment. This iterative process continues until one obtains the desired number of significant digits.

-For example, if we analyze the initial results of the first formula Bauer and Ramanujan, we see that the second value uses 3 terms: in fact, the first value was not able to give one significant digit of the number Pi, we doubled the increment that increases from 1 to 2, and so the next iteration uses 3 terms (1 + increment value). By the same principle as the second value has not only brought a new significant figure, it also doubled the increment which now goes from 2 to 4 and thus the next iteration request 7 words (3 + increment value). And so on.

-How does one decide whether a new value brings significant figure? Simply by comparing the integer part of the logarithm to the base 10de the absolute error of the iteration couranteavec the integer part of the base 10 logarithm of the absolute error of the previous iteration. If these two quantities are equal, doubling the increment. Obviously, in the first iteration, there is no absolute error of the previous iteration; therefore it is necessary to set this amount to the value (Which is quite logical since it is somehow the maximum error that can have).

Note2: To calculate the logarithm base 10, you use the function log10 of the C library to get the integer part, simply to make an explicit conversion like this: (int) log10 (yourvariable).

Note3:

Now how does one decide the number of significant figures to calculate? Simply by comparing the absolute error of the previous iteration with accuracy chosen initially. We distinguish two cases:

-for the first two formulas (Bauer / Ramanujan and Euler) converging very slowly, precision will be used to 1e-4 (#define EPSILON1 1e-4).

-for the last two formulas, precision is used to 1e-14 (#define EPSILON21e-14).

note4:

For the release of the first two formulas, use the conversion specification %9d to print the number of employed and the conversion specification .4lf% To print the value and error. For the output of both last formulas, use the specification% 2d conversion to print the number of employed and the conversion specification% .14lf to print the value and error.

note5:

Use the following value for the number : M_PI constant defined in

note6 :

Use the double type for your calculations because we need a fairly high accuracy.

note 7:

In summary, your main() function will consist of four almost identical loops to produce the results according to different formulas (the precision used, the function call to use and impressions of formats change, but the method is the same for all loops). Each of your functions must not use other functions except function sqrt (otherwise there will be penalty).

(personal note: the functions wont paste here so i screened shot them..sorry!