PLEASE NOTE: I only need help with Questions (d) and (e). Please provide the Matlab code for the problem and plotting the graph. If possible, please also provide the code for graphing the true percent relative error.

Here are the solutions to Questions (a), (b), and (c) from another Chegg Solution:

a) for low reynolds number we get that v= g/18(_s-)d^2

and for high reynolds number v=square root of (4g(_s-)d/3C_d)

now C_d= 24/Re + 3/Re^-2 +.34

putting C_d in the second equation we get

v=square root of (4g(_s-)d/3[24/Re + 3/Re^-2 +.34])

putting Re=dv/ we get

v=square root of (4g(_s-)d/3[24/dv + 3^-2/(dv)^-2 +.34])

or v=square root of (4gd(_s-)/3[24/dv+3^-2^-2/(dv)^-2 +.34)

b) using P8.48.2 we know that

v= g/18(_s-)d^2 =9.81/18(7.874-1)200*10^-6= 749.27*10^-6 units

c) Re= dv/= 1*200*10^-6* 749.27*10^-6 /.014= 1.07*10^5

that means flow is turbulent.

So, using Re we get Cd= 24/1.07*10^5 +3/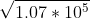 +.34 = .349224

Determining the velocity of particles settling through fluids, like the falling sphere example, is of importance to many areas of engineering and science. Such calculations depend on the flow regime, as represented by the dimensionless Reynolds number, Re: Repud where p is the fluid's density [kg/m], d is the particle diameter [m], v is the particle's settling velocity [m/s], and u is the fluid's dynamic velocity [N-s/m). Under laminar conditions (Re